ml 3gff 20011030

ml - Introduzione interattiva di MATLAB Vai all'indice del corso

Grafici di funzioni riguardanti la fisica
Versione 0.7

Indice del modulo

3gff.00 - Grafici di funzioni riguardanti la fisica
3gff.05 - Costanti fisiche fondamentali
3gff.06 - Fattori di conversione
3gff.30 - Relativita` ristretta. Dilatazione dei tempi e contrazione delle lunghezze
3gff.32 - Trasformazioni speciali di Lorentz
3gff.40 - Scattering della radiazione elettromagnetica nell'effetto Compton
3gff.41 - La legge di Planck
3gff.51 - Statistica di Boltzmann
3gff.52 - Statistica di Bose - Einstein
3gff.53 - Statistica di Fermi - Dirac
3gff.54 - Statistiche di Boltzmann, Bose e Fermi a confronto
3gff.60 - Grafici di polinomi di Hermite

3gff.00 - Grafici di funzioni riguardanti la fisica

Puo` essere molto utile servirsi di MATLAB per familiarizzarsi anche con le funzioni riguardanti la fisica. Anche per queste funzioni si possono incontrare i problemi riguardanti punti singolari come quelli associati alla divisione per lo zero ed i problemi delle approssimazioni numeriche. Ora si trattano espressioni che forniscono grandezze e quindi si deve curare la scelta attenta delle unita` di misura e dei relativi fattori di conversione.

torna all'indice del modulo - del corso

3gff.05 - Costanti fisiche fondamentali

Con le seguenti frasi definiamo alcune costanti di interesse generale che si incontrano piu` spesso nelle formule della fisica. Tra i sistemi di unita` di misura privilegiamo il Sistema Internazionale, SI. Per le costanti fondamentali utilizziamo degli identificatori il cui significato manterremo invariato in tutte le elaborazioni che seguono.

>> cvl = 2.99792458e8;         % vel. luce [ m s^-1 ]
>> me = 9.109534e-31;          % massa elettrone [ kg ]
>> ec = 1.6021892e-10;         % carica elettrone [ C ]
>> hpl = 6.626176e-34;         % costante di Plank [ J s ]
>> hta = 1.0545887e-34;        % h / 2 pi [ J s ]
>> Ggr = 6.6720e-11;           % costante di gravitazione universale [N m^2 kg^-2 ]
>> ggr = 9.8062;               % accelerazione di gravita` [ m s^-2 ]
>> Nav = 6.022045e23;          % numero diAvogadro [ mol^-1 ]
>> Rgas = 8.31441;             % costante universale dei gas [ J mol^-1 K^-1 ]
>> kblz = 1.300662e-23;        % costante di Boltzmann [ J K^-1 ]
>> sigsb = 5.67032e-8;         % costante di Stefan - Boltzmann [ W m^-2 K^-4 ]
>> alfam1 = 137.03604;         % inversa della costante di struttura fine 
>> Roo = 1.097373177e7;        % costante di Rydberg [ m^-1 ]
>> a0 = 5.2917706e-11;         % raggio di Bohr [ m ]
>> Far = 9.648476e4;           % costante di Faraday [ C mol^-1 ]
>> c1pl = 3.741832e-16;        % prima costante di Planck per la radiazione [ W m^2 ]
>> c2pl = 1.438786e1;          % seconda costante di Planck per la radiazione [ m K ]
>> mubo = 9.274078e-24;        % magnetone di Bohr [ J T^-1 ]
>> munu = 5.050951e-27;        % magnetone nucleare [ J T^-1 ]
>> mup = 1.4106171e-26         % momento magnetico del protone [ J T^-1 ];

torna all'indice del modulo - del corso

3gff.06 - Fattori di conversione

Con frasi analoghe alle precedenti definiamo i piu` importanti tra i fattori di conversione tra unita` di misura. Anche per questi fattori utilizziamo degli identificatori di uso riservato. Questi nomi sono formati da due parti separate da ``_`` che individuano le due misure omogenee poste in collegamento; il numero puro definito e` il rapporto tra la prima grandezza e la seconda.

>> kg_eVsuc2 = 5.609e35;         % 1 eV/c^2  / 1 kg  [ unita` di massa ]
>> eVsuc2_kg = 1.783e-36;        % 1 eV/c^2  / 1 kg  [ unita` di massa ]
>> J_eV = 6.241e18;              % 1 J / 1 eV [ unita` di energia ]
>> eV_J  = 1.602e-19;            % 1 eV / 1 J [ unita` di energia ]
>> kgmsus_eVsuc  = 1.871e27;     % 1 kg m s^-1 / 1 eV c^-1 [ unita` di quantita` di moto ]
>> eVsuc_kgmsus  = 5.345e-28;    % 1 eV c^-1 / 1 kg m s^-1 / [ unita` di quantita` di moto ]

torna all'indice del modulo - del corso

3gff.30 - Relativita` ristretta. Dilatazione dei tempi e contrazione delle lunghezze

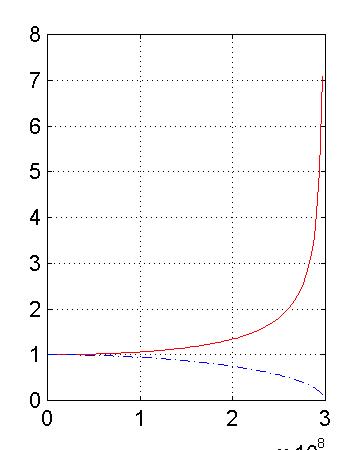
Si osservino i grafici che forniscono dilatazione dei tempi e contrazione delle lunghezze passando da un riferimento proprio ad un riferimento inerziale.

>> beta = 0:0.01:0.99;
>> t0 = 1; tv = t0 ./ sqrt(1 - beta.^2);
>> l0 = 1; lv = l0 .* sqrt(1 - beta.^2);
>> plot(beta,tv,'b',beta,lv,'r')
>> xlabel('0 \leq {\it\beta = v/c} \leq 1')
>> ylabel('{\itt} (m) e {\itl} (s)')
>> legend('{\itt} = {\itt_0} / sqrt(1-{\it\beta}^2)', '{\itl} = {\itl_0} * sqrt(1-{\it\beta}^2)', 2)
>> title('Contrazione delle lunghezze e dilatazione dei tempi', 'FontSize', 12, 'Color', [0 0.5 0], 'FontAngle', 'italic', 'FontWeight', 'bold')

torna all'indice del modulo - del corso

3gff.32 - Trasformazioni speciali di Lorentz

Si osservino i grafici delle funzioni x^2 e radice quadrata.

>> 
>>

torna all'indice del modulo - del corso

3gff.40 - Scattering della radiazione elettromagnetica nell'effetto Compton

L'interazione tra la radiazione elettromagnetica ed elettroni liberi può essere descritta in termini di urto elastico tra fotoni (visti come particelle di massa zero e quantità di moto p = h / λ) ed elettroni. Applicando il principio di conservazione della quantità di moto e dell'energia, si ottiene la relazione di Compton:

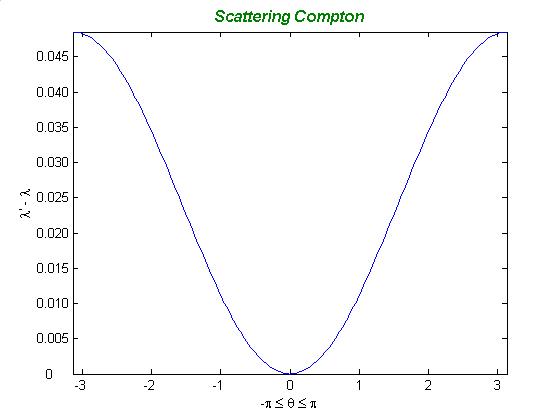
λ' - λ =λ_C(1 - cosθ) ,

dove λ_C = h / m_ec = 0.024262 Å, λ è la lunghezza d'onda della radiazione incidente e λ' la lunghezza d'onda della radiazione deviata dell'angolo θ rispetto alla direzione d'incidenza.

Si noti come la differenza λ' - λ sia nulla per la radiazione che non subisce interazione (θ = 0), mentre sia massima per θ = ± p (il fotone 'rimbalza' indietro), assumendo il valore di 2λ_C @ 0.05 Å. Questo comunque piccolo valore fa sì che il fenomeno risulti più sensibile per le radiazioni di lunghezza d'onda inferiori all'Ångstrom, tipicamente X e g.

>> lCompton = hpl/(me*cvl) * 10^10;    %2.4262e-2;    %in Angsrtom
>> teta = -pi:0.01*pi:pi;
>> lambda = lCompton * (1 - cos(teta));
>> plot(teta, lambda);
>> xlabel('-\pi \leq \theta \leq \pi')
>> ylabel(texlabel('lambda'' - lambda'))
>> title('Scattering Compton', 'FontSize', 12, 'Color', [0 0.5 0], 'FontAngle', 'italic', 'FontWeight', 'bold')
>> axis tight

torna all'indice del modulo - del corso

3gff.41 - La legge di Planck

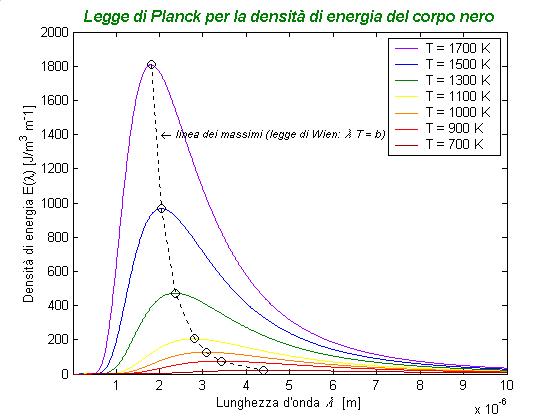
La distribuzione della densità di energia in funzione della frequenza (espressa in J/m³ m^-1) per la radiazione di corpo nero è data dalla legge di Planck:

dalla risulta evidente la dipendenza dalla lunghezza d'onda l e dalla temperatura T.

Nel grafico sono riportate diverse distribuzioni della densità di energia per diverse temperature. Si noti come il massimo di E(l ) risulti via via più piccolo e spostato verso le alte lunghezze d'onda, man mano che la temperatura diminuisce.

I massimi di E( l ) sono determinati dalla legge di Wien: l _MaxT = b, con b = hc / 4.9651K.

>> lam = 1e-8:1e-8:1e-5;
>> T = [1700 1500 1300 1100 1000 900 700];
>> k1 = hpl*cvl;
>> k2 = 8*pi*k1;
>> for i = 1:7; E(i,:) = k2 ./ lam.^5 * 1 ./ (exp(k1./(lam * kblz * T(i))) - 1); end
>> h = plot(lam,E); hold on
>> 
>> %Cosmetica
>> Viola = [0.75 0 1];
>> Verde = [0 0.6 0];
>> Giallo = [0.9 0.9 0];
>> Arancio = [1 0.5 0];
>> RossoScuro = [0.75 0 0];
>> set(h(1), 'Color', Viola)
>> set(h(2), 'Color', 'b')
>> set(h(3), 'Color', Verde)
>> set(h(4), 'Color', Giallo)
>> set(h(5), 'Color', Arancio)
>> set(h(6), 'Color', 'r')
>> set(h(7), 'Color', RossoScuro)
>> xlabel('Lunghezza d''onda {\it\lambda} [m]')
>> ylabel('Densità di energia E({\lambda}) [J/m^3 m^-1]')
>> axis([-Inf 1e-5 -Inf 2000])
>> s1 = 'T = '; s2 = ' K';
>> legend([s1 num2str(T(1)) s2], [s1 num2str(T(2)) s2], [s1 num2str(T(3)) s2], 
[s1 num2str(T(4)) s2], [s1 num2str(T(5)) s2], [s1 num2str(T(6)) s2], [s1 num2str(T(7)) s2])
>> title('Legge di Planck per la densità di energia del corpo nero', 'FontSize', 12, 'Color', 
[0 0.5 0], 'FontAngle', 'italic', 'FontWeight', 'bold')
>> %Massimi (legge di Wien)
>> lamM = k1 ./ (4.9561 * kblz * T);
>> Emax = k2 ./ lamM.^5 * 1 ./ (exp(4.9561) - 1);
>> plot (lamM,Emax,':ko')
>> text(2.05e-6,1400,'\leftarrow {\itlinea dei massimi (legge di Wien: \lambdaT = b)}', 'FontSize', 8)
>> hold off

torna all'indice del modulo - del corso

3gff.51 - Statistica di Boltzmann

La statistica di Boltzmann si applica a sistemi di particelle distinguibili (come le molecole di un gas, a qualsiasi temperatura) e ha la forma:

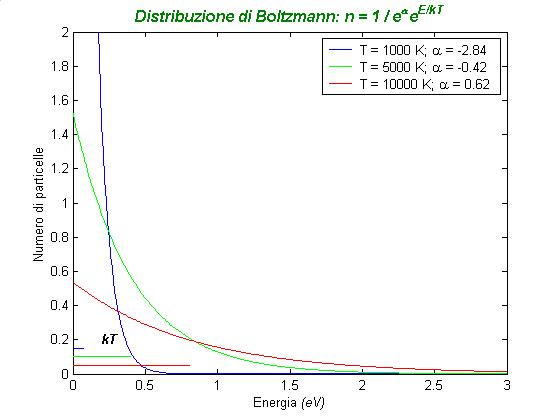
n_Boltz(E) = 1 / e^a e^{E / kT} ,

dove n_Boltz(E) è il numero di particelle che hanno energia E, k è la costante di Boltzmann, T la temperatura di equilibrio del sistema, e a una costante che dipende dal numero totale di particelle nel sistema, e che viene quindi fissata per normalizzare la distribuzione: l'integrale tra 0 e +¥ di n_Boltz(E) corrisponde al numero totale di particelle.

Nel grafico sono riportate le distribuzioni di Boltzmann per tre differenti temperature (e tre differenti valori di a, in modo che il numero di particelle sia lo stesso nei tre casi).

Questa distribuzione è un'esponenziale pura, che si riduce di un fattore 1/e per ogni aumento pari a kT in energia (nel grafico è riportato in basso a sinistra la dimensione di kT per i tre casi).

>> E = 0:0.01:3;
>> T = [1000 5000 10000];
>> nT = size(T,2);
>> alpha = [-2.84 -0.42 0.62];
>> for i = 1:nT; nblz(i,:) = 1 ./ exp(alpha(i) + E./(kblz*J_eV * T(i))); end
>> h = plot(E, nblz); hold on
>> axis([0 3 0 2])
>> kT = kblz*J_eV * T;
>> for i = 1:nT
xkT(i,:) = 0:kT(i):kT(i);
ykT(i,:) = (0.2 - 0.05*i) * ones(1, size(xkT,2));
h(i) = plot(xkT(i,:), ykT(i,:));
end
>> hold off

torna all'indice del modulo - del corso

3gff.52 - Statistica di Bose - Einstein

La statistica di Bose si applica a sistemi di particelle indistinguibili che non obbediscono al principio di esclusione (come il gas di fotoni o di fononi), dette anche bosoni, caratterizzate dall'avere spin nullo o intero.

La distribuzione ha la forma:

n_Bose(E) = 1 / (e^a e^{E / kT} - 1),

con lo stesso significato dei simboli visto per la distribuzione di Boltzmann.

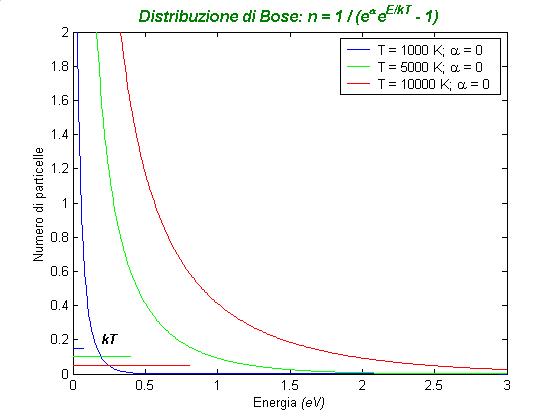
Nel grafico sono riportate le distribuzioni di Bose per tre differenti temperature (ma tutte con lo stesso valore di a = 0, valido in particolare per il gas dei fotoni, dunque non normalizzate).

Per energie sufficientemente grandi questa distribuzione approssima l'esponenziale di Boltzmann, in quanto il termine e^a e^{E / kT} sovrasta il termine -1; invece, alle basse energie (rispetto a kT), il numero di particelle risulta maggiore che nella distribuzione di Boltzmann, a causa del termine -1 a denominatore, e tende addirittura a +¥ quando l'energia tende a zero.

>> E = 0:0.01:3;
>> T = [1000 5000 10000];
>> nT = size(T,2);
>> alpha = [0 0 0];
>> for i = 1:nT; nbos(i,:) = 1 ./ (exp(alpha(i) + E./(kblz*J_eV * T(i))) - 1); end
>> h = plot(E,nbos); hold on
>> axis([0 3 0 2])
>> kT = kblz*J_eV * T;
>> for i = 1:nT
xkT(i,:) = 0:kT(i):kT(i);
ykT(i,:) = (0.2 - 0.05*i) * ones(1, size(xkT,2));
h(i) = plot(xkT(i,:), ykT(i,:));
end
>> hold off

torna all'indice del modulo - del corso

3gff.53 - Statistica di Fermi - Dirac

La statistica di Fermi - Dirac si applica a sistemi di particelle indistinguibili che obbediscono al principio di esclusione (come il gas di elettroni), dette anche fermioni, caratterizzate dall'avere spin semi-intero.

La distribuzione ha la forma:

n_Fermi(E) = 1 / (e^a e^{E / kT} + 1),

con lo stesso significato dei simboli visto per la distribuzione di Boltzmann e di Bose.

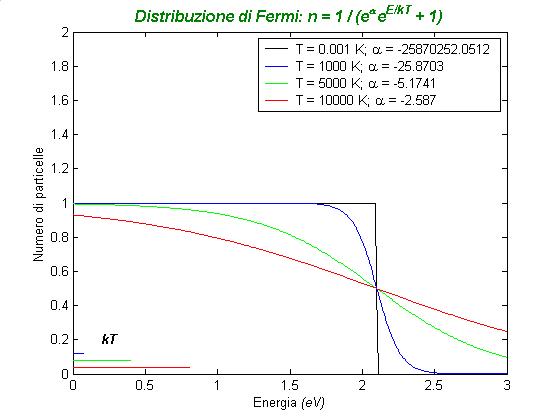
Nel grafico sono riportate le distribuzioni di Fermi per tre differenti temperature. Il parametro a non è stato fissato con condizioni di normalizzazione, ma considerando il caso particolare del gas di elettroni, con una densità elettronica simile a quella del potassio e corrispondente a un valore per l'energia di Fermi dato da E_F = -a kT = 2.1 eV.

Si noti come, in questo caso la distribuzione possa essere riscritta come:

n_Fermi(E) = 1 / (e^{(E - E}F^{) / kT} + 1) ,

e dunque come per E = E_F si abbia invariabilmente n_Fermi(E) = 1/2, cioè il numero medio di particelle che occupa il livello di energia corrispondente all'energia di Fermi è esattamente 1/2.

Si noti anche come per T tendente a zero, il sistema tende a riempire, con una sola particella, tutti i livelli di energia inferiore a E_F, e a lasciare vuoti i livelli superiori, minimizzando così l'energia del sistema prossimo allo zero assoluto, in conformità con il principio di esclusione.

Per energie sufficientemente grandi anche questa distribuzione approssima l'esponenziale di Boltzmann, mentre alle basse energie (rispetto a kT) il numero di particelle risulta comunque non superiore a uno (sempre in accordo con il principio di esclusione).

>> E = 0:0.01:3;
>> T = [0.001 1000 5000 10000];
>> nT = size(T,2);
>> Ef = 2.1;
>> alpha = - Ef ./ (kblz*J_eV * T);
>> for i = 2:nT; nfer(i,:) = 1 ./ (exp(alpha(i) + E./(kblz*J_eV * T(i))) + 1); end
>> h = plot(E, nfer); hold on
>> axis([0 3 0 2])
>> kT = kblz*J_eV * T;
>> for i = 1:nT
xkT(i,:) = 0:kT(i):kT(i);
ykT(i,:) = (0.2 - 0.04*i) * ones(1, size(xkT,2));
h(i) = plot(xkT(i,:), ykT(i,:));
end
>> hold off

torna all'indice del modulo - del corso

3gff.54 - Statistiche di Boltzmann, Bose e Fermi a confronto

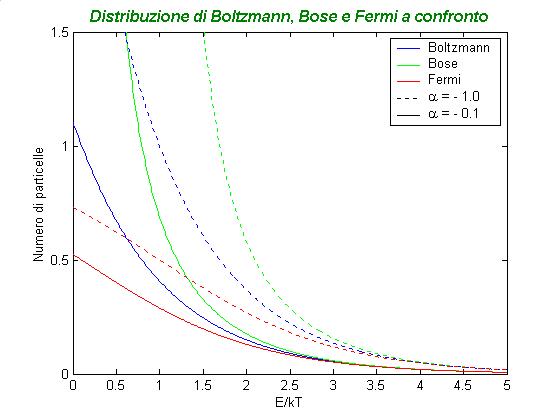
Le tre distribuzioni sono messe a confronto nel seguente grafico. Si è usata E/kT come variabile indipendente e si sono usati due valori per a: -1.0 e -0.1.

Si noti come traslando verso destra le curve tratteggiate di (-0.1) - (-1.0) = 0.9 unità, si ha la sovrapposizione con le curve a linea continua.

>> E_su_kT = 0:0.01:5;
>> alpha = [-1.0 -0.1];
>> for i = 1:size(alpha,2)
nblz(i,:) = 1 ./ exp(alpha(i) + E_su_kT);
nbos(i,:) = 1 ./ (exp(alpha(i) + E_su_kT) - 1);
nfer(i,:) = 1 ./ (exp(alpha(i) + E_su_kT) + 1);
end
>> plot(E_su_kT, nblz(2,:), '-b'); hold on
>> plot(E_su_kT, nbos(2,:), '-g')
>> plot(E_su_kT, nfer(2,:), '-r')
>> zero = zeros(1, size(E_su_kT,2));
>> h1 = plot(E_su_kT, zero, ':k');
>> h2 = plot(E_su_kT, zero, '-k');
>> plot(E_su_kT, nblz(1,:), ':b')
>> plot(E_su_kT, nbos(1,:), ':g')
>> plot(E_su_kT, nfer(1,:), ':r')
>> axis([0 5 0 1.5])
>> set(h2, 'LineStyle', '-')
>> xlabel('E/kT')
>> ylabel('Numero di particelle')
>> legend('Boltzmann', 'Bose', 'Fermi', '{\alpha} = - 1.0', '{\alpha} = - 0.1')
>> title('Distribuzione di Boltzmann, Bose e Fermi a confronto', 'FontSize', 12, 'Color', [0 0.5 0], 'FontAngle', 'italic', 'FontWeight', 'bold')
>> hold off

torna all'indice del modulo - del corso

3gff.60 - Grafici di polinomi di Hermite

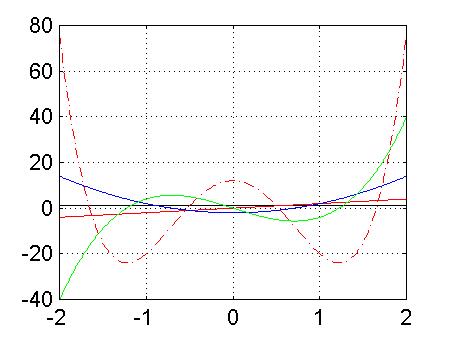
Si osservino i grafici dei polinomi di Hermite Hn(x) per n=0,1,...,4 .

>> x=-5:0.01:5;
>> H0(size(x))=0; H0=H0+1; H1=2*x;
>> H2=2.*x.*H1-2;
>> H3=2.*x.*H2-4.*H1; 
>> H4=2.*x.*H3-6.*H2;
>> plot(x,H0,'-k',x,H1,'-r',x,H2,'-b',x,H3,'-g',x,H4,'-.r')
>> grid on

torna all'indice del modulo - del corso