ml 1vet 20011103

ml - Introduzione interattiva di MATLAB Vai all'indice del corso

Vettori - prime nozioni
Versione 0.8

Indice del modulo

1vet.10 - Coppie numeriche e vettori piani
1vet.12 - Terne numeriche e vettori spaziali
1vet.33 - Vettori paralleli - Prodotto di uno scalare per un vettore
1vet.34 - Moltiplicazione di una sequenza numerica per un fattore di conversione
1vet.35 - Somma e differenza di vettori
1vet.37 - Combinazioni lineari di vettori
1vet.40 - Prodotto scalare di vettori
1vet.41 - Simmetria e bilinearita` del prodotto scalare
1vet.42 - Calcolo del prodotto scalare
1vet.50 - Norma di un vettore
1vet.51 - Versori
1vet.52 - Una richiesta di controllo su vettori
1vet.55 - La function sum applicata ad un vettore
1vet.57 - Norme p di un vettore
1vet.58 - Norme infinite di un vettore
1vet.60 - Prodotto vettore di vettori tridimensionali
1vet.61 - Calcolo del prodotto vettore

torna all'indice del modulo - del corso

1vet.10 - Coppie numeriche e vettori piani

Le coppie di numeri reali, cioe` le sequenze di numeri reali di lunghezza 2, si possono interpretare come punti del piano cartesiano, ovvero come vettori del piano cartesiano.
Osserviamo che tali entita` si possono interpretare anche come numeri complessi.

Si notino in particolare i punti con distanza 1 dall'origine, cioe` i vettori di modulo 1, che appartengono agli assi Ox ed Oy: li indicheremo rispettivamente con e_x ed e_y, ovvero equivalentemente con e₁ ed e₂.

In MATLAB sono ottenuti scrivendo [1 0] e [0 1].

torna all'indice del modulo - del volume

1vet.12 - Terne numeriche e vettori spaziali

Le terne di numeri reali, cioe` le sequenze di numeri reali di lunghezza 3, si possono interpretare come punti dello spazio tridimensionale riferito ad un sistema di assi cartesiani, ovvero come vettori dello spazio vettoriale tridimensionale.

Si notino in particolare i punti con distanza 1 dall'origine, cioe` i vettori di modulo 1, che appartengono agli assi Ox, Oy ed Oz: li indicheremo rispettivamente con e_x, e_y ed e_z, ovvero equivalentemente con e₁, e₂ ed e₃.

In MATLAB sono ottenuti scrivendo [1 0 0], [0 1 0] e [0 0 1].

torna all'indice del modulo - del volume

1vet.33 - Vettori paralleli - Prodotto di uno scalare per un vettore

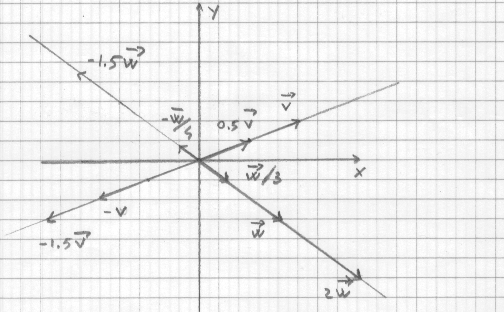
Il prodotto di un numero s per un vettore v, riga o colonna, e` il vettore simile a v ottenuto da questo moltiplicando per lo scalare s tutte le sue componenti.

Geometricamente la moltiplicazione per uno scalare trasforma un vettore in uno parallelo; per i vettori in due dimensioni la cosa risulta ben evidente.

>> v=[2.5,1];
 0.5*v
ans =
    1.2500    0.5000
>> -1*v
ans =
   -2.5000   -1.0000
>> -v
ans =
   -2.5000   -1.0000
>> -1.5*v
ans =
   -3.7500   -1.5000
>> v*(-1.5)
ans =
   -3.7500   -1.5000

torna all'indice del modulo - del volume

1vet.34 - Moltiplicazione di una sequenza numerica per un fattore di conversione

Una frequente applicazione del prodotto di uno scalare per un vettore riguarda la trasformazione di una sequenza di misure relativa ad una prima unita` di misura u nelle corrispondenti misure relative ad una seconda unita` U: in questi casi si devono moltiplicare le prime misure per il fattore di conversione U/u.

>> Lire = [18200 98000 164500];
EDU» LirePerEuro = 1936.27;
EDU» Euro = [9.6 50 86];
EDU» Lire = Euro * LirePerEuro
Lire =
  1.0e+005 *
    0.1859    0.9681    1.6652
EDU» format bank
EDU» Lire = Euro * LirePerEuro
Lire =
      18588.19      96813.50     166519.22

L'esempio precedente mostra anche l'utilita` della richiesta format bank per la scrittura di dati finanziari.
Osserviamo anche che rappresentare due vettori paralleli come i precedenti nello stesso spazio non ha grande interesse in quanto riguardano misure non omogenee; inoltre le componenti dei precedenti vettori ML riguardano oggetti fisici diversi, non ha interesse sottoporre il loro spazio vettoriale a trasformazioni come le rotazioni e quindi ha poco interesse collocare i suddetti vettori in tale spazio.

torna all'indice del modulo - del volume

1vet.35 - Somma e differenza di vettori

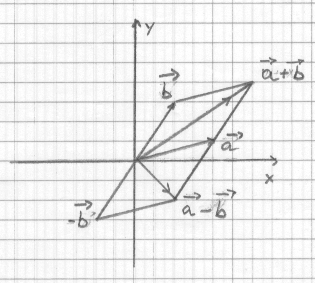
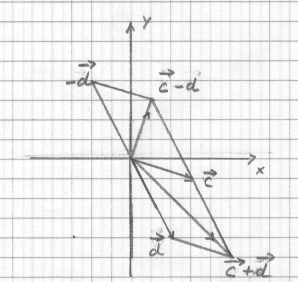
La somma di due vettori simili si ottiene sommando le componenti corrispondenti; la differenza sottoponendo a sottrazione le componenti omologhe. Geometricamente la somma fornisce il vettore che corrisponde alla diagonale che inizia nell'origine del parallelogramma costruito sui due vettori addendi. La differenza fornisce il vettore analogo ottenuto similmente dal primo addendo e dall'opposto del secondo.

>> a=[2,0.5];
>> b=[1,1.5];
>> a+b
ans =
     3     2
>> a-b
ans =
     1    -1
>> c=[0.5 1.5]
c =
    0.5000    1.5000
>> d=[1 -2];
>> c+d
ans =
    1.5000   -0.5000
>> c-d
ans =
   -0.5000    3.5000
>>

torna all'indice del modulo - del volume

1vet.37 - Combinazioni lineari di vettori

I vettori, dato che si possono moltiplicare per scalari e sommare, si possono sottoporre a combinazione lineare. Gli insiemi delle combinazioni lineari di dati vettori di un certo spazio costituiscono i sottospazi di tale spazio. In particolare le combinazioni lineari di due vettori non paralleli dello spazio tridimensionale costituiscono il piano per l'origine contenente i due vettori.

Servendosi di MATLAB si possono chiarire le caratteristiche di questi piani.

In particolare si considerino i piani delle combinazioni lineari
del vettore [1,0,0] e del vettore [0,0,2];
del vettore [1,1,0] e del vettore [0,0,2];
del vettore [1,1,0] e del vettore [3,0,3];
del vettore [1,1,1] e del vettore [-2,2,2];
del vettore [1,1,1] e del vettore [2,-2,-2].

torna all'indice del modulo - del volume

1vet.40 - Prodotto scalare di vettori

Per prodotto scalare (o prodotto interno, o dot product) di due vettori dello spazio tridimensionale v e w si intende il prodotto dei moduli dei due vettori per il coseno dell'angolo che i due vettori formano. Noi lo indicheremo con (v,w).

Il prodotto scalare ha una interpretazione geometrica abbastanza evidente.

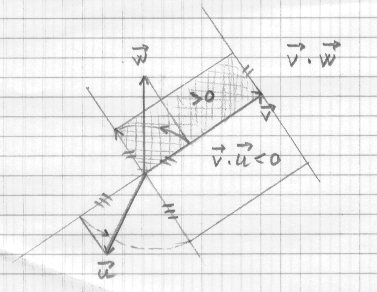
E` chiaro che il prodotto scalare di due vettori non nulli e` nullo sse (= se e solo) essi sono ortogonali, e` positivo sse formano un angolo minore di pi/2, e` negativo sse formano un angolo maggiore di pi/2.
E` chiaro anche che il prodotto scalare e` una composizione simmetrica, cioe` che (v,w) = (w,v).

Il prodotto scalare si puo` considerare un operatore che a due vettori associa uno scalare. Esso si puo` equivalentemente considerare come una funzione di due variabili vettoriali con valori scalari. Le funzioni di questo tipo, cioe` aventi come dominio l'insieme delle coppie di vettori e come codominio l' insieme degli scalari, sono chiamate anche forme.

torna all'indice del modulo - del volume

1vet.41 - Simmetria e bilinearita` del prodotto scalare

Dalla definizione si deduce che il prodotto scalare e` un operatore bilineare, cioe` che (cv+c'v',w) = c(v,w)+c'(v',w) e quindi per la simmetria (v,dw+d'w') = d(v,w)+d'(v,w').
Esprimiamo allora i due vettori operandi come combinazioni lineari dei tre versori:
v = v₁ e₁ + v₂ e₂ + v₃ e₃v2 v = v₁ e₁ + v₂ e₂ + v₃ e₃v2
ed utilizziamo la bilinearita` del prodotto scalare ed il fatto che (_e_i,_e_j) = dk_i,j ed otteniamo
(v,w) = v₁ w₁ + v₂ w₂ + v₃ w₃.
Quindi il prodotto scalare si esprime come la somma dei prodotti delle componenti corrispondenti dei due vettori. Osserviamo che in questa espressione si possono verificare abbastanza agevolmente la simmetria e la bilinearita` del prodotto scalare.

torna all'indice del modulo - del volume

1vet.41 - Calcolo del prodotto scalare

Con MATLAB si puo` chiedere il prodotto scalare di un vettore riga per un vettore colonna con lo stesso numero di componenti.

>> a=[2,0 5];
>> b=[1,1 5]';
>> a*b
ans =
     27

Lo stesso risultato si ottiene applicando la function dot fornendole i due vettori riga come argomenti

>>  a=[2,0.5,1]; 
>>  b=[1,1.5,-1];
>>  dot(a,b)     
ans =
    1.7500

torna all'indice del modulo - del volume

1vet.50 - Norma di un vettore

Si dice lunghezza euclidea o norma 2 di un vettore con componenti reali [v1, v2, ..., vn] la radice quadrata della somma dei quadrati delle componenti. Il prodotto scalare di un vettore con il proprio trasposto fornisce il quadrato della lunghezza euclidea. Tale lunghezza, cioe` la norma 2, si ottiene anche applicando la function norm.

>> v=[2,1,-.5];
>> norm(v), sqrt(v*v')
ans =
       2579132
ans =
       2.27912

torna all'indice del modulo - del volume

1vet.51 - Versori

Si dice versore ogni vettore con norma pari ad 1.
Ogni vettore di uno spazio sui reali e` parallelo a due versori, anzi a due. Essi si possono ottenere dividendo tutte le componenti del vettore rispettivamente per la sua norma e per la sua norma cambiata di segno.
Viceversa ogni vettore si puo` esprimere come prodotto della sua norma (e della sua norma cambiata di segno) per un versore.

>> v=[2,0,5];
>> nv = norm(v)
nv =   
     5.3852
>>u = v/nv
u =
      0.3714         0    0.92855
>> nu=norm(u)
nu  =
        .00001

torna all'indice del modulo - del volume

1vet.52 - Una richiesta di controllo

Presentiamo ora richieste analoghe alle precedenti seguite da una richiesta per il controllo della uguaglianza del vettore v dato con il versore parallelo moltiplicato per la sua norma nv

>> v=[2,0.1,50];
>> nv = norm(v) 
nv  =
   50.0401
>> u = v/nv 
u =
  0.0400    0.0020    0.9992
>> nu=norm(u)
nu =
      1
>> v-nv*u
ans =
   1.0e-16 *
         0   -0.1388         0

La scrittura ottenuta non deve stupire. Esprime un vettore con componenti molto piccole, vicine a eps, e questo manifesta che si ha l'uguaglianza nei limiti della precisione dei calcoli effettuati.

torna all'indice del modulo - del volume

1vet.55 - La function sum applicata ad un vettore

Un richiamo della function sum avente come argomento un vettore riga fornisce la somma delle componenti del vettore.

>> v = -1:2:7
v   =
       -1      1      3     5     7
sum(v)
ans =
        15

Questa function e la length consentono di calcolare la media dei valori delle componenti di un vettore.

>> sum(v)/length(v)
v   =
       3

torna all'indice del modulo - del volume

1vet.57 - Norme p di un vettore

Se p e` un numero positivo, si dice norma p di un vettore con componenti reali v = [v1, v2, ..., vn] la radice p-esima della somma delle potenze p-esime dei valori assoluti delle componenti. Questo valore si ottiene con il comando della forma norm(v,p).

Si osserva che questa nozione di norma generalizza quella di norma 2 e che il richiamo norm(v) porta allo stesso valore del richiamo norm(v,2).
Inoltre norm(v,1) fornisce la somma dei valori assoluti delle componenti di v e se v ha solo componenti positive, fornisce lo stesso valore di sum(v).

>> v = -1:2:7
v   =
       -1      1      3     5     7
norm(v,1)
ans =
        15

torna all'indice del modulo - del volume

1vet.58 - Norme infinite di un vettore

MATLAB consente di chiamare la function norm con primo argomento un vettore e secondo argomento inf o -inf.
Il richiamo norm(v,inf) fornisce il massimo dei valori assoluti delle componenti di v.
Il richiamo norm(v,-inf) fornisce il minimo dei valori assoluti delle componenti di v.

>> norm([23 -120 66],inf)
ans  = 
         120
>> norm([23 -120 66],-inf)
ans  = 
         23

torna all'indice del modulo - del volume

1vet.60 - Prodotto vettore di vettori tridimensionali

Per prodotto vettore (o prodotto esterno, o cross product) di due vettori dello spazio tridimensionale v e w si intende il vettore ortogonale ai vettori operandi avente come modulo il prodotto dei moduli dei due vettori per il seno dell'angolo che i due vettori formano e diretto nella direzione tale che la terna dei due operandi e del risultato sia destrorsa, cioe` una persona posta nella direzione del vettore risultato veda ai suoi piedi i due vettori operandi disposti da sinistra a destra.

Il prodotto vettore ha quindi una interpretazione geometrica un po' complessa.

E` chiaro che il prodotto vettore di due vettori non nulli e` nullo sse (= se e solo) essi sono paralleli

torna all'indice del modulo - del volume

1vet.61 - Calcolo del prodotto vettore

Con MATLAB si puo` chiedere il prodotto vettore con la function cross.

>> a=[2,0.5,1];
>> b=[1,1.5,-1];
>> cross(a,b)
ans  =
      -2.0000    3.0000    2.5000

torna all'indice del modulo - del volume