No Title

ISBA is about to enter a new millennium and its ninth year of promoting the development and application of Bayesian statistical theory and methods useful in the solution of theoretical and applied problems in science, industry and government. For many ISBA members, including myself, conveying the advantages of Bayesian theory and methods in their substantive discipline is both demanding and rewarding. Drawing the attention of the wider scientific community to the attractions of Bayesian approaches requires a different set of skills. So it was with great pleasure that American members of ISBA, in particular, welcomed the article that appeared in the November 19, 1999, issue of Science, the widely known flagship publication of the American Association for the Advancement of Science. The five-page article appears in the ``News Focus'' section of the journal. Written by David Malakoff, it is titled ``Bayes Offers a 'New' Way to Make Sense of Numbers.'' AAAS members, or nonmembers for $5, can download the article from www.sciencemag.org/ content/vol286/issue5444.

The article features innovative Bayesian methods in many scientific disciplines, including environmental science, medicine, engineering, and genomics. The applications discussed include decision making in clinical drug trials, the interpretation of evidence in court, management of wildlife populations, and (yes) Microsoft's animated paperclip. The article builds on interviews with quite a few members of ISBA. Significantly for ISBA, it emphasizes the conundrum that many of us face in education. On the one hand, undergraduates find it straightforward to condition on observables and express probabilities about conjectures, but find p-values counterintuitive. On the other hand, students need frequentist tools and language in a world that is becoming more Bayesian but still has a long way to go. Given the resource constraints of most academic institutions, this presents challenges for Bayesians involved in formal teaching.

The tone and substance of the Science article reflect the tremendous advance in Bayesian methods and applications during the 1990's. It also shows that there is a long way to go. Perhaps most important, however, the article is an illustration of the importance of effective and clear communication across the sciences. It is a good inspiration for some professional New Years resolutions.

There were 145 ballots returned. Of these 19 were were deemed invalid as no name was placed on the envelope (or inside) that would allow them to be validated as coming from an ISBA member. All names were checked against the membership list. The ballots and envelopes were separated and then the votes were tallied. The counting was carried out by the Executive Secretary.

The results of the elections are:
228 President-Elect
Alicia Carriquiry
228 4 Board Members
(alphabetical order)
Deborah Ashby
Dani Gamerman
Dalene Stangl
Mark Steel

Once again we had a very impressive list of candidates with all receiving a substantial number of votes. Congratulations to the winners and thanks to all for participating.

Next year will be very important as well: our world meeting will be held in Greece and it is going to be one of the largest Bayesian gatherings ever (but the largest will be at Valencia 7, if Bernardo's forecast in this issue is right ...); ``we are in the advent of a Bayesian era'' (as confirmed by Berger in his interview ...) and, finally, the year 2000 will be important (at least for those of us who are calling themselves mathematicians) because the International Mathematical Union, with the support of UNESCO, has launched the World Mathematical Year 2000 (see wmy2000.math.jussieu.fr for more details).

As of January, 1st, 2000, ISBA will have a new President: Phil Dawid is replacing John Geweke, the author of a thoughtful article in this issue. Alicia Carriquiry is the new President-Elect (becoming the President in the year 2001) whereas Susie Bayarri, Past-President (and main responsible for my appointment as Editor ...), is leaving the Executive Committee. Tony O'Hagan is the Vice Program Chair for 2000. Finally, Deborah Ashby, Dani Gamerman, Dalene Stangl and Mark Steel are replacing Daniel Peña, Enrique de Alba, Ed George and Malay Ghosh as Board members.

Our aims about the Newsletter (NL) were made very clear in our first issue when we said that ``we would like the NL to become a valuable source of information and a place for discussion''. We hope that the former is true, at least partially, for someone, whereas we are still far from achieving the latter. We continue pursuing our goal of promoting communications among Bayesians; we encourage ISBA members to send us comments, letters, books (yes, a Book reviews section could be started as someone asked me) and use the other tools ISBA provides, like the ISBA/SBSS Archive for Abstracts at www.isds.duke.edu/isba-sbss/.

In the meanwhile, we are already working for the next issue: Colin McCulloch is going to write on ``Template Mixture Models for Image Region Analysis'', whereas Renate Meyer is writing her report on ``Bayesians in New Zealand'' and Gabriel Huerta his own on software developed by Radford Neal. Other topics will be announced on the ISBA Newsletter web page at www.iami.mi.cnr.it/isba as soon as they will be available.

With the advent of the next millennium, it is worth pausing for a moment and trying to have a glimpse on what will be the future of Bayesianism. Jim Berger will help us in doing so. Jim (www.isds.duke.edu/~berger) is The Art and Sciences Professor of Statistics at the Institute of Statistics and Decision Sciences, Duke University. Formerly, he was at Purdue University and did all his education at Cornell. His outstanding contributions to the field and service to the profession are well-known to us. His recent JASA 2000 vignette (to appear in 2000) motivated the following e-interview.

I was in the mathematics Ph.D. program at Cornell, and was lucky that there were outstanding statisticians in the department, in particular Larry Brown (who became my advisor), Jack Kiefer, Roger Farrell, and Jack Wolfowitz. Math Ph.D. students are typically much too theoretical for their own (or anyone's) good, and I was no exception, but the group at Cornell got me going in the right direction.

I certainly knew of Bayesian analysis as a graduate student. In particular, my area of research was statistical decision theory (admissibility, etc.), and many of the basic technical tools in the area involve Bayesian analysis. Nevertheless, the overall atmosphere at Cornell at the time was staunchly frequentist, and so I graduated as a frequentist.

When I arrived at Purdue, Herman Rubin almost immediately made Bayesianism seem respectable to me; especially persuasive were his reminiscences of the extensive efforts by himself, Wald and others (and eventually Savage) to justify non-Bayesian statistics in the late 40's and early 50's, and how they instead found that `all roads led to Bayesianism.' My own early research was primarily on frequentist shrinkage estimation, and there I also found that all roads led to Bayesianism. Finally, in writing my 1980 book on statistical decision theory, I had to take a hard look at fundamental ideas myself and, before long, was calling myself a Bayesian.

There is a clear change in the emphasis from your 1980 book to your 1985 book. Could you comment on that?

By the time of the 1980 book, I was calling myself a Bayesian (which, incidentally, is the only useful criterion I know for classifying someone as a Bayesian). Yet I certainly did not think like a typical Bayesian; in particular, I did not automatically think in a conditional sense, as do naturally-trained Bayesians. Shortly after the 1980 book came out, I realized I had to come to grips with conditioning, and embarked on an extended effort to do so. This resulted in my book with Robert Wolpert on the Likelihood Principle in 1984 (second edition in 1988), and led to an extensive rewriting of the decision theory book, in which it became much more Bayesian. (Amusingly, shortly after the 1985 edition was published, I received a letter from the Springer editor saying that he had received numerous requests to have the first edition reprinted - the second edition had become too Bayesian!)

I should maybe comment a bit more on `coming to grips with conditioning.' I never stopped being a frequentist, in the sense that I have always felt it to be obvious that one should care about the long run performance of statistical procedures. Thus `coming to grips with conditioning' meant my coming to an understanding concerning the right mix of conditional and frequentist thinking in statistics. My current view as to the right mix is something like 85% conditional (Bayesian) thinking and 15% frequentist thinking, although I've lately been hearing things from people like Jayanta Ghosh, Jamie Robins and Larry Wasserman that are causing me to shift the frequentist component upwards.

The two books discussed above probably had the most impact, but they were, of course, primarily reinterpretations of what had gone before in the field. From about 1985-1995, I
ISBA Newsletter, December 1999 INTERVIEWS

Another long-term interest has been the unification of statistical methodology, in the sense of finding methodology that produces answers that simultaneously have reasonable Bayesian and frequentist interpretations. On the Bayesian side, this largely motivated my work on objective Bayesian inference (a subject on which I am supposedly writing a book, with Jose Bernardo and Dongchu Sun); on the frequentist side, this motivated my work on the conditional frequentist paradigm, which basically shows that, by appropriate conditioning, frequentists can typically arrive at the same conclusions as objective Bayesians.

One probably always likes one's latest work best (in fact, I can usually only remember my latest work), and most of my recent papers have been in the area of model selection and model criticism. I am quite enamored with intrinsic Bayes factors (developed initially with Luis Pericchi), expected posterior priors (with Jose Miguel Perez), and partial posterior predictive p-values (with Susie Bayarri).

In your JASA vignette, you mention that we may be in danger of losing Bayesian analysis to other disciplines, as we have lost other areas of statistics. Could you give examples and ways of avoiding such danger?

How this has repeatedly happened in statistics is too big a topic. But, even within Bayesian statistics, a lot of this has gone on. Filtering in signal processing has always been highly Bayesian (essentially finding the posterior mean of the signal), although usually it is not stated as such. Hierarchical or multilevel modeling provides the statistical basis of analysis in numerous disciplines, yet its essential origin in the Bayesian viewpoint is often ignored. Luckily, the success of MCMC has, at least temporarily, brought many of these `wandering communities' back into the fold.

In other areas we have not been so lucky. Data-mining is an area, with many Bayesian connections, that we have probably lost, in the sense that it is now perceived as being primarily in the domain of computer science. Graphical models is at risk; it was primarily started by statisticians (many of them Bayesian), so that it is still associated with statistics, but it is rapidly being gobbled up by the computer science/engineering community.

I never really thought much about how we can avoid such things. Science and engineering may be undergoing a reorganization, with Information Sciences increasing in prominence as a separate scientific division. Positioning statistics centrally within this division, by working closely with computer scientists and others, could be the long-term solution (e.g., with data-mining `assigned' to Statistics, within this reorganization). I can imagine ISBA doing things to help. For instance, it could start sections on graphical models (or, indeed, on hierarchical modeling or signal processing), with the idea of trying to keep a significant identification of the area with (Bayesian) statistics. ISBA journals could also help (see below).

There you distinguish five classes of Bayesian analysis: objective, subjective, robust, frequentist-bayes and pseudo-bayes? Do you think they will coexist?

First, a comment on terminology: I used the term `pseudo-Bayes' to reflect the type of Bayesian analysis one commonly sees today, in which priors are specified very casually, without any clear motivation (subjective or
ISBA Newsletter, December 1999 INTERVIEWS

As to whether these classes will all coexist, my reaction is - of course! I can not imagine any of them disappearing, because they each have central roles to play in at least some of the arenas in which Bayesian statistics is used. One of my pet peeves is the all-too-common insistence that some particular one of these is the real purview of Bayesian statistics, with the others being misbegotten relatives. I am delighted with them all!

What will be the areas that will be more active within our field? Which developments are still lacking? Which application areas need our attention?

Hey, I couldn't even answer that in the much longer JASA vignette! Besides, such predictions are historically rather worthless. For instance, I can imagine a future (based on what Mike West tells me) in which the majority of Bayesian activity is in bioinformatics, something that, at the moment, is not much more than a large blip on the Bayesian radar screen. I can also imagine a future in which most everything is operated on the basis of Bayesian expert systems. I can even imagine a future in which 90% of all statistical analyses are not based on p-values. (Okay, that one is a stretch.)

We have recently seen ads on fuzzy-logic based dishwashing machines and cameras. Shall we soon see Bayesian refrigerators or video games?

Many machines will likely run on Bayesian logic, but I doubt if the name `Bayesian' will be useful as a public marketing tool (at least until it becomes associated with the wealth of a few billionaires).

An amusing thought, but it probably won't happen, in part because there has never been a single non-Bayesian approach to a problem. On the other hand, we probably need to start using more detailed identifiers for our Bayesian articles (e.g. `A quasi-Bayesian approach to ...'), since the Bayesian literature is becoming so huge.

There is one aspect of the distinction between Bayesian and non-Bayesian articles that is going to have to be addressed by the profession relatively soon. To this day, articles of each type are primarily judged in their own arena. Thus a non-Bayesian article that proposes new methodology must compare that methodology with existing non-Bayesian methodology, but is rarely asked to provide a comparison with existing Bayesian methodology. If journals were to begin to require such cross- paradigm comparisons, the effect would be profound (and to the great benefit of Bayesian statistics). And many of the forces at work today are pushing statistics in that direction (the computational advances making Bayesian methodology readily accessible; the extensive development of objective Bayesian methodology; etc.).

ISBA's major role must be in enhancing communication among Bayesians. The newsletter is a great start. I briefly talk about a journal below. It would also be nice to find structures in which other groups of Bayesians could be formally included into ISBA. The geographical ISBA chapters are nice - we should have more. Also, as mentioned above, I would love to see sections based
ISBA Newsletter, December 1999 INTERVIEWS

Do you think a Bayesian journal, possibly supported by ISBA, might be a good idea?

I have always thought that this would be a great idea. The objections to a Bayesian journal arose primarily from statisticians, the argument being that creating a specialty journal would reduce the visibility of Bayesian articles and undermine our statistics-wide aspirations. I never accepted even this argument against a Bayesian journal but felt that, in any case, it ignores one of the primary functions of ISBA, which is to provide an organization for non-statisticians who have a major interest in Bayesian analysis. Non-statisticians are unlikely to scan the huge statistics literature to find the Bayesian articles, and many would love the convenience of a Bayesian journal. Indeed, I hope to see a future in which ISBA publishes many journals, focusing, say, on particular application areas of Bayesian analysis.

Starting a Bayesian journal is not only right from the viewpoint of scientific communication, but it would probably be the major factor in future growth of ISBA. It is time to take up this idea again.

What about teaching. Most statistical teaching is still non-Bayesian. Not so long ago, I even suffered some anti-Bayesian courses. Shouldn't we more actively promote Statistics courses with a Bayesian flavour, even at an introductory level?

I'm surprised to hear that you encountered actual anti-Bayesian courses (you are not that old!) Here at Duke, most of our courses - even elementary courses - have at least a strong Bayesian flavor. But in primarily non-Bayesian departments, it is much harder to work Bayesian courses into the curriculum.

For graduate courses, there is no longer a shortage of Bayesian textbooks, but there is a severe time shortage. Statistics is broadening, becoming more computational and interdisciplinary, both of which exert pressure on the number of `traditional' statistics courses that can be taught. This makes it difficult for a graduate program to add a strong Bayesian component. Luckily, Bayesian analysis is at the forefront of much of the computational and interdisciplinary developments, so sneaking Bayesian analysis in through this `back door' may be the best current option (until faculties become significantly more Bayesian).

For elementary courses, there is still a shortage of Bayesian textbooks, in the sense that there is not a wide selection available for tailoring the courses to the students and the existing realities of `service course' teaching (in the USA anyway). For instance, an elementary textbook on objective Bayesian analysis could readily replace standard texts in introductory service courses, in that students would be learning mostly the same methods, but would be introduced to the much easier to understand Bayesian interpretation of these methods. Software is, of course, also an issue in all of this, but that will sort itself out.

Thanks Jim for a very thought-provoking conversation. Readers may have access to the mentioned references through Jim's web page mentioned above. Any comments on this interview will be welcome at my e-address above. ISBA Newsletter, December 1999 BAYESIAN HISTORY

I have often been asked about the origin of the Valencia meetings. As time passes, the number of active researchers among those who came to the first meeting, 20 years ago, is obviously getting pretty thin. Thus, I enthusiastically accepted the suggestion of Raquel Prado to record that story for the ISBA newsletter.

The first thoughts of what would eventually become the Valencia meetings came in the Summer of 1976. I had just finished my Ph.D. at University College London, which Dennis Lindley, as Head of the Department of Statistics, had converted into the European Bayesian department of the early 70's. The atmosphere there was great: Phil Dawid and Mervyn Stone were faculty members; visitors during that period included most European and many American Bayesians; at any time there were about dozen research students mostly working within a Bayesian framework; every week the `journal club' provided an informal seminar where new ideas were tried and discussed; Adrian Smith and I were among the last students who Dennis Lindley supervised before his early retirement, and we had become good personal friends. At University College the world looked Bayesian; thus, it came as a kind of a shock to discover that in most statistical conferences you had to fight for your right to work within Bayesian statistics to a mainly unsympathetic audience, with no real time left to go into the details of your work. At Dennis's suggestion, I then attended what I believe was the very first international workshop solely devoted to Bayesian Statistics.This was a European conference on New Developments in the Applications of Bayesian Methods (Aykac and Brumat, 1977), sponsored by INSEAD, a French business school, and held in Fonteainebleau, near Versailles, in June 1976. In what to me was a very memorable occasion, I drove Dennis Lindley and Bruno de Finetti to a cosy French restaurant, where we shared a most interesting lunch; after a long debate on the necessity or not of $\sigma$ -additivity, the conversation moved towards the special atmosphere in the conference, where you no longer have to defend your Bayesian position, but could explain your work to colleagues who took for granted that the Bayesian viewpoint was, at least, a reasonable alternative. The three of us were convinced that it would be a good idea to try to establish some form of periodic Bayesian forum.

A year later, in April 1977, I attended an international conference on the Foundations of Statistical Inference held in Florence. The lively discussions among Bayesians at that meeting suggested again the convenience of a dedicated conference. Shortly after the Florence meeting, I got a Postdoctoral Fellowship to spend the 1977-78 academic year at the Department of Statistics of Yale University, a Bayesian stronghold at the time, with Richard Savage as chairman and John Hartigan teaching what must have been one of the first advanced graduate courses on Bayesian Statistics. During these months I was invited to give seminars at many North American universities with a Bayesian presence; thus, I visited Dick Barlow at Berkeley, George Box at Madison, Morrie DeGroot at Pittsburgh, Art Dempster at Harvard, Seymour Geisser at Minneapolis, Jack Good at Blacksburg, John Pratt at MIT, Jim Press at Riverside, Cesareo Villegas at Vancouver, and Arnold Zellner at Chicago. With Morrie DeGroot, there was an immediate powerful common empathy; during a very long evening, with plenty of scotch, we talked about many aspects of life and somehow, by dawn, we came to talk about statistics, and we agreed to make an effort to try to organize an international Bayesian meeting at the first available occasion. I immediately contacted Dennis Lindley and Adrian Smith and they were both enthusiastic. It was agreed that I would explore the possibilities of organizing this in Valencia. Back to Spain in the Fall of 1978, I was appointed to the newly created Chair of Biostatistics of the University of Valencia. Spain had just emerged from a period of repulsive dictatorship, and the Spanish
ISBA Newsletter, December 1999 BAYESIAN HISTORY

The new chair of Biostatistics, physically located at the School of Medicine, created the conditions to work with a small bunch of young graduates in mathematics whom I got interested in Bayesian statistics. These included Carmen Armero, Susie Bayarri, José Bermúdez, Juan Ferrándiz, Lluis Sanjuan, Maite Rabena and Mario Sendra. The atmosphere was very attractive, both professionally and personally: we were all young, curious, energetic leftwingers in a country moving fast forward. When I told them about the meeting they all reacted fervently. Most of the available funds were needed to contribute to travel and accommodation expenses of the invited speakers, so that we had to take on all of the administration burdens ourselves, at that time without the benefits of e-mail or even fax. The organization of the first Valencia meeting was a team effort of this group. The Valencia meetings would not have existed without this team.

The self-appointed programme committee for this first meeting consisted of Morrie DeGroot, Dennis Lindley, Adrian Smith and myself. Publicity was mainly by word of mouth. The meeting was held in Hotel Las Fuentes, a beach hotel in Alcossebre, about 100 km. north of Valencia, from May 28th to June 2nd, 1979. It was a rather remote place so that transportation from Valencia airport had to be provided (some people tried to go there on their own, by train, and were left at a deserted railway stop in the middle of the fields, 6 km. away from the hotel!) We had 28 invited lectures, all followed by invited discussions, and no contributed papers.This was attended by 93 people from 13 countries, and it is probably fair to say that these people included most of the better known Bayesians at the time. The meeting was organized into early morning and late afternoon sessions, with plenty of time during the day for informal discussions by the pool, or at the beach. At night many of us moved on to the local disco `El Lobo' until late, but we were all ready for work first thing in the morning. On the last day of the conference we had an assembly where people unanimously declared that the experience had been too good to leave without the promise of a continuation. It was decided that a period of four years would be appropriate to allow time for new ideas to appear, and it was agreed that the same committee would try to organize it again in Valencia with a view to create a series, in the spirit of the Berkeley symposia. After the conference dinner, George Box sung to the audience There's No Theorem Like Bayes'Theorem, a version of Irving Berlin's ``There's No Business Like Show Business." This was the origin of the Valencia cabarets, a tradition which has been kept in all Valencia meetings. The Proceedings, (Bernardo et al., 1980), today a Bayesian collector ``must'', with the presented papers and their discussion, (and even the George Box song!) were published by the University of Valencia Press and reprinted as a special issue by the Spanish journal of statistics Trabajos de Estadística, the predecessor of Test. The first proof-reading, at a time when TEX did not exist, was a nightmare supported by the same local team who made the conference possible in the first place. The idea of purely Bayesian meetings started to gather momentum. The first conference on Practical Bayesian Statistics was held in Cambridge, UK, in 1982 (Dawid and Smith, 1983). This was the occasion where the second Valencia meeting was tentatively announced as an example of the sure-thing principle: the Spanish general elections were about to take place; if the conservatives won, they had already funded Valencia 1 and it was a success, so one may expect a second funding; if the socialists won, they were supposed to be especially sensitive to Bayesian Statistics,
ISBA Newsletter, December 1999 BAYESIAN HISTORY

The third meeting was planned for June 1987, roughly four years after Valencia 2 but back to our preferred June date. A federal system of government was by then established in Spain, and the conference was basically funded by the (socialist) government of the State of Valencia. The location of the first two meetings was closed for renovation, so that we had to find an alternative.

We very much wanted to keep the original idea of a Mediterranean beach hotel and found an attractive location in the south. The third meeting was held at Hotel Cap Negret, in Altea, 120km. south from Valencia, from June 1st to 5th, 1987. This was attended by 196 people from 23 countries, a 51% size increase from Valencia 2. The invited programme contained 31 invited papers, followed by invited discussions, and we repeated the successful after-dinner contributed paper parties. The Proceedings of Valencia 2 had been a commercial success for the publisher (the committee agreed to renounce to royalties in favour of a lower selling price) and we were in a position to choose. Among several offers, we preferred that of Oxford University Press. The Proceedings of Valencia 3 (Bernardo et al., 1988) contain the invited papers, their discussion, and a selection of 28 contributed papers which, in what seemed routine by now, only made it in after a fierce competition.

The fourth meeting was originally planned for June 1991 and was to be organized by the same committee. However, the whole statistical community was saddened by the death of Morrie DeGroot in 1989. The remaining committee members invited Jim Berger to join in and continue Morrie's work. Moreover, Dennis Lindley expressed his desire to step down from committee duties so he was named Conference President, and Phil Dawid was invited to join the committee. At that time, I had temporarily left the university to accept the post of Chief Statistical Adviser to the Government of the State and, as a consequence, the dates of the meeting had to be advanced by a couple of months to avoid their clash with the State elections. Finally, the expected number of delegates suggested that previous locations were not big enough, so we have to find a new beach location. The fourth Valencia meeting, dedicated to the memory of Morrie DeGroot, was held at Hotel Papa Luna, in Peñiscola, 140km. north from Valencia, from 15th to 20th April, 1991. This was attended by 286 people from 33 countries, a 46% size increase from Valencia 3. The invited programme contained 30 invited papers, followed by invited discussions, and the by now famous after-dinner contributed papers parties. For the first time the meeting was not held in summer (some people ignored this piece of
ISBA Newsletter, December 1999 BAYESIAN HISTORY

The Valencia International meetings have been attended by scholars from 49 countries, namely, Argentina, Australia, Austria, Belgium, Brazil, Canada, Chile, China, Cuba, Czechkia,
ISBA Newsletter, December 1999 BAYESIAN HISTORY

At Valencia 6, it was decided to enlarge to conference committee to include Susie Bayarri, David Heckerman and Mike West. Thus, the conference committee for the Seventh Valencia International Meeting on Bayesian Statistics consists of Susie Bayarri, Jim Berger, Jose Bernardo, Phil Dawid, David Heckerman, Dennis Lindley (Conference President), Adrian Smith and Mike West.

The conference will be organized in early June, 2002, at a location yet to be determined. A naïve quadratic projection suggests that about 575 people may attend (more sophisticated predictions are welcome!)

Meeting	Year	Size
Valencia 1	1979	93
Valencia 2	1983	130
Valencia 3	1987	196
Valencia 4	1991	286
Valencia 5	1994	376
Valencia 6	1998	459
Valencia 7	2002	575?

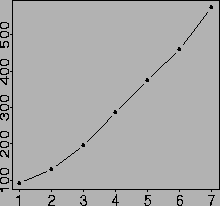$\psfig{file=9912-bernardo.ps,height=5cm,width=5cm,angle=-90}$ Evolution of the number of delegates at the Valencia meetings

As all ISBA members should be aware, ISBA decided to have their world meetings every four years in coordination with the Valencia meetings. Thus, we may expect a major Bayesian conference every two years: we will soon have the next ISBA world meeting in Crete, June 2000; this will be followed by Valencia 7, June 2002, and by another ISBA world meeting in June 2004.

The Valencia meetings have now a web site, with a mirror in the States. These will be periodically updated as the organization of Valencia 7 progresses.

www.uv.es/~bernardo/ valenciam.html www.stat.duke.edu/~bernardo/ valenciam.html

If you have not attended Valencia 6, or have moved since that meeting, (and thus you are not automatically included in the current mailing list), but you may be interested in attending Valencia 7, or if you just want to be included in the conference mailing list, please e-mail me (jose.m.bernardo@uv.es) the following information: Name, affiliation, postal address, telephone, fax, e-mail, web page, area(s) of interest.

Aykac A., and Brumat C. (eds.) (1977) New Developments in the Applications of Bayesian Methods. Amsterdam: North-Holland.

Bernardo, J.M., Berger, J.O., Dawid, A.P. and Smith, A.F.M. (eds.) (1992). Bayesian Statistics 4. Oxford: Oxford University Press.

Bernardo, J.M., Berger, J.O., Dawid, A.P. and Smith, A.F.M. (eds.) (1996). Bayesian Statistics 5. Oxford: Oxford University Press.

Bernardo, J.M., Berger, J.O., Dawid, A.P. and Smith, A.F.M. (eds.) (1999). Bayesian Statistics 6. Oxford: Oxford University Press.

Bernardo, J.M., DeGroot, M.H., Lindley, D.V. and Smith, A.F.M. (eds.) (1980). Bayesian Statistics. Valencia: University Press.

Bernardo, J.M., DeGroot, M.H., Lindley, D.V. and Smith, A.F.M. (eds.) (1985). Bayesian Statistics 2. Amsterdam: North-Holland.

Bernardo, J.M., DeGroot, M.H., Lindley, D.V. and Smith, A.F.M. (eds.) (1988). Bayesian Statistics 3. Oxford: Oxford University Press.

Cervera, J. L. and Muñoz, J. (1996). Proper scoring rules for fractiles. Bayesian Statistics 5,513-519. Oxford: Oxford University Press.

Dawid, A. P. and Smith, A. F. M. (eds.) (1983). 1982 Conference on Practical Bayesian Statistics. The Statistician 32, Numbers 1 and 2. ISBA Newsletter, December 1999 APPLICATIONS

Were athletes in the 1920's or the 1950's as good as current athletes? Few topics in sports invoke as much passion as how players from different eras compare. Many arguments are undertaken about players from separate eras. Comparing a player from the 1920's and the 1990's is difficult, and seemingly impossible. Any comparison of their statistics is completely flawed because they played against different competition, with different rules, different equipment, and different societal pressures. I want to know how the two players would compare, if they were playing at their peak, at the same time. It may be that players from past eras were more influential and their ``accomplishments'' were more significant, but my interest is in directly comparing their physical abilities-a time machine that removes a player from his era and places him in the era of another player to compare them directly. How does one compare them, faced with these unlevel ``playing fields?''

Shane Reese, Pat Larkey, and I utilize Bayesian procedures to compare players from different eras (We have an article describing this work in the September 1999 issue of JASA). We study ice hockey, golf, and baseball. For ice hockey we rate players on their ability to score points (goals + assists). We have data on all National Hockey League forwards from 1948-1996. In golf we study the ability of players to score well. We have the scores of all players from the four golf majors, US Open (1935-1997), Masters (1935-1997), the Open Championship (1961-1997), and the PGA Championship (1961-1997). In baseball we study both home run hitting and hitting for average. We have data for all hitters from 1901-1996.

We form a Bayesian bridge from era to era. Although a player in the 1920's never played against contemporary players, they did play against players, who played against players, who played against players, ... , who played against contemporary players. For example, Babe Ruth never played with Mark McGuire, but he did play with Jimmie Fox, who played with Ted Williams, who played with Mickey Mantle, who played with Hank Aaron, who played with Reggie Jackson who played with Mark McGwire. This overlapping of players forms the bridge from one era to another. A complication in this bridge is that players were not the same age while their careers overlapped. We set up an additive model to estimate the effect of each year in the range of our data. We also have an age effect for each sport. This additive model estimates the effect of each season, age, and the ability of each player, simultaneously. This is crucial to the model-we do not want adjustments made to the statistics without everything being adjusted.

Two crucial aspects of the model benefited a great deal from the Bayesian approach. We model the distribution of players with a hierarchical model. We also model the effects of age (the age function) with a hierarchical model. The peak ability of each player is modeled as coming from a distribution of players. This distribution, labeled the talent pool, is clearly changing through time. To account for this we allow the hyperparameters of the hierarchical distribution to change over time. Not all players age the same way within each sport-though there is clearly a similarity in aging patterns. We used this information, and fit a hierarchical distribution of aging curves. The rate of maturing and declining is represented by a parameter within the model. These parameters are modeled with a hierarchical distribution. This hierarchical modeling of a player's peak ability and age function had intuitive ramifications. There are a number of players who have limited data, either because they are new and have not participated very long in sports, or for whatever reason they did not play very long. Tiger Woods, the young golf phenomenon was a prime example of this. Our data was through the 1997 season, which was Woods' first full pro season. In the 1997 Masters he broke the scoring record and won the tournament by a record 12 strokes. He also performed well in the three

other majors in 1997-yet he was only 21 years old! The aging function in golf has peak performance in the low thirties (31 is peak). The average golfer is about a shot and a half worse per round, than peak performance, when he is 21. Thus, if Woods were to age the same as the ``average'' professional golfer he would be by far the best golfer ever. Due to the hierarchical age function and the hierarchical peak performance distribution, the model estimates that Woods will be very good, but he will not age the same as the average professional golfer. He is closer to his peak performance than the average 21 year old professional.

This regressing to the mean, in both the aging function and peak performance so beautifully demonstrates the strength of hierarchical models. Based on the distribution of golfers being so tightly grouped it is extremely unlikely that this one human is so much better than everyone else. It is much more likely, because it is much more common in golf, that he ``matured'' well and is much closer to his peak. This estimate is a combination of Woods' data, the ability of all golfers, and the aging pattern of all golfers. There are examples similar to this regression to the mean phenomenon in each sport.

The average aging functions for each sport fit closely with conventional wisdom. Ice hockey, which is more physically demanding than the other sports has a sharper peak, with a more rapid decline than either golf or baseball. Baseball had a sharper decline than golf.

In his book, Full House: The spread of excellence from Plato to Darwin, Stephen Jay Gould conjectures that talent pool is getting better in every sport. He believes that there is essentially a limit, or wall, of human athletic performance. Throughout time, with the increase in the size of the population there will be a higher proportion of players closer to the wall. We found some evidence for his theory. In each of the sports players are getting better, and clearly the median-type player is getting better faster through time. The golf example agrees closely with this theory. The best players in the game in each era are getting slightly better, they are generally of comparable ability, but the bottom level players in each era are getting much better. A median-type player in the 1950's is estimated to be more than one shot worse per round than current golfers. This difference is so large that a median player from the 1950's would not be good enough to play on the professional tours in 1990.

While we were mainly interested in the effects of age and the changing population within each sport, the question of who would be the best in each sport if they all played at the same time, is irresistible. In golf the top players are (with their estimated scoring average if they were at their peak in the 1997 Masters in parentheses) Jack Nicklaus (70.42), Tom Watson (70.82), Ben Hogan (71.12), Nick Faldo (71.19), and Arnold Palmer (71.33). In ice hockey the best point scorers of all time are (with estimated points, at peak, in 1996) Mario Lemieux (187), Wayne Gretzky (181), Eric Lindros (157), Jaromir Jagr (152), and Paul Kariya (129). For batting average the top five are (with estimated batting average, at peak, in 1996) Ty Cobb (.368), Tony Gwynn (.363), Ted Williams (.353), Wade Boggs (.353), and Rod Carew (.351). For home run hitting the top five are (with estimated proportion of home runs, at peak, in 1996) Mark McGwire (.104), Juan Gonzalez (.098), Babe Ruth (.094), Dave Kingman (.093), and Mike Schmidt (.092).

So, we are able to reconstruct Babe Ruth and move him from his era to the current era, or likewise to any era. While we cannot watch Babe Ruth hit home runs, we do have a Bayesian reconstruction of him.

While academicians decry their own inabilities to assess personal probabilities for real quantities of interest, I have found industrial practitioners quite able and keen to do so, with help at elicitation from a supportive statistician. Industrial managers are well
ISBA Newsletter, December 1999 APPLICATIONS

aware that immense quantities of information are embedded in their skilled workforce, and they are eager to ensure that it is used to the full in the valuation and quality assurance of the company products.

I shall describe here two useful applications of subjectivist methods, one in the warranting of whiteware production, and another in product design in the automobile tire industry. As is common in competitive industries, names and specific statistical detail must be suppressed, but a flavor of the activity can be usefully presented.

Quality whiteware (washing machines, dishwashers, ranges, and clothes dryers) are typically warranted by leading companies against breakdown in home use for one year or two. The self-insuring firm is keen to have a precise idea of how many of its machines will fail within warranty time, and the reasons and costs for the required repairs. Such knowledge is crucial to the economic assessment of the warranty program. Production processes today make extensive use of statistical tests along the production line itself to limit the risk of failure of items installed in a home. But despite extreme care, failures do occur, even the rare dreaded item found ``dead-on-arrival'' in a home.

Statistics on failures are collected as a matter of routine in the procedure for the company's reimbursing the technician who makes the repairs. The time and the reason for failure as well as components replaced, along with an estimate of the number of cycles the machine has run must be noted on a card mailed or e-mailed to the quality assessment division of the factory. Thus, for every batch of machinery sold, a data file is kept identifying the date of sale of the machine along with the failure date, if any.

Failures are typically assessed with a mixture of Weibull distributions, one portion representing recognition of the dead-on-arrival and early burnout syndromes, and the other portion for the more typical unseemly wearout or burnout failure in normal use. For the simplest products, the analysis of observations regarded exchangeably, mixed over five parameters suffices for useful uncertainty assessment and continual updating. But larger representations involving eight or even eleven can be handled simply in the way I shall now describe.

In practice. there is really little need in such a problem for fanciful MC computations, as a grid for each parameter over a range of ten or so selected possibility values is quite adequate. In all such assessment design decisions, simplicity and immediacy of interpretation are much more important to the production manager than is precise accuracy to even the second decimal place, not to speak of the third.

The assessment of the initial mixing functions is easily done based on the experience of the production manager who is familiar with conditions under which the batch of items has been produced. Familiarity with the power of data to inform posterior distributions for failures from previous machine types and batches is actually helpful for managers to assess the power of what they know about the present machine type. Moreover, when a new production model design is undertaken, the testing from the design stage and the knowledge of the practical reasons for the changes from the old design are typically helpful in the assessment of the initial mixing distribution over failures from the new design. ``Nuff said.''

A pleasing experience in the tire industry occurred when raw material import changes necessitated a new tyre design based on two possible choices over each of four factors. A non-textbook problem, massive experimental cost considerations allowed that not even one replication of each of the 16 possible designs could be afforded! Most amusing was the plant manager's concern, after puzzling on his own over a statistical design cookbook, as to ``how can the book identify a rule for which tyres to test without even assessing what we know and don't know about tyres?'' The end to a long story involved two of the factory's expert tyre sensors spending some ten hours apiece over the course of two weeks doing their best at answering pointed questions regarding the relations between four by two different tyre design specifications and the ride, handling, and noise experience of the designed tyres under road conditions. Elicitation techniques were based on
ISBA Newsletter, December 1999 APPLICATIONS / TEACHING

Whereas academicians apparently have ample time to bemoan the deplorable position of one required to make debatable value and belief judgments, practitioners of industrial engineering seem much more willing to plunge in and to do what needs to be done. In fact, they are quite used to being in this situation enumerable times in any working day vis-a-vis a variety of matters! No one can be criticized for being uncertain. Of course, modulo cost efficiency of further information gathering, one attempts to be informed, even with formal statistical information whenever possible.

But recognizing our uncertainties and acting responsibly in the face of them, without recourse to magical metaphysics of ``the men in white coats,'' is a practical course for quality product improvement that is motivated by the operational subjective statistical method. The subjectivist understanding of statistical procedures actually empowers industrial practitioners by recognizing explicitly that it is their own uncertain knowledge judgments that are being used, not some formidable mysteries accessible only to the ordained. The interested reader may enjoy more extensive methodological details and motivation in my book, Operational Subjective Statistical Methods: a mathematical, philosophical, and historical introduction, New York: John Wiley, 1996, ISBN 0-471-14329-0.

I have been teaching for the ASA's LearnSTAT program. This is a program that takes successful JSM short courses and puts them on the road. I am teaching ``An Introduction to Bayesian Methods in Biostatistics''. I will most likely offer the course in 5 different cities in 1999/2000. I presented in Alexandria on October 1 and in Santa Monica on December 6. The motivation behind offering this course is to increase the understanding and use of Bayesian methods by applied statisticians working in health-related research. The course is targeted at applied statisticians working in medical research, government regulatory agencies, private pharmaceutical companies, and other health-related institutions. It is also appropriate for graduate students who do not get exposure to Bayesian methods in their curriculum.

Here is a general outline of the topics covered.

1. Introduction

$\bullet$ Bayes theorem
$\bullet$ Prior, Likelihood, Posterior
$\bullet$ Examples: GUSTO Revisited by Reverend Bayes (Brophy and Joseph) - Discover '96 (Wills)

2. Priors (reference, conjugate and other) and Elicitation

3. Calculation of Posteriors and Predictive Distributions

$\bullet$ conjugate
$\bullet$ Laplace
$\bullet$ MCMC

4. Decision Analysis

5. Software examples (Context: many of examples used above)

$\bullet$ Minitab Macros - Jim Albert
$\bullet$ S-plus
$\bullet$ Bugs - Gilks, Spiegelhalter, Best, et al.

6. Foundations: Classical versus Bayesian paradigm

$\bullet$ Definition of probability
$\bullet$ Centrality of likelihood principle
$\bullet$ Inferential differences

All topics are taught via examples. The examples are drawn primarily from Bayesian Biostatistics edited by Berry and Stangl, Marcel Dekker 1996. The book is offered with the course.
ISBA Newsletter, December 1999 BIBLIOGRAPHY

$\bullet$ B. STORER(1989). Design and Analysis of Phase I Clinical Trials. Biometrics, 45, 925-937.

This paper may be of interest, although it is not using the Bayesian approach, as it compares traditional designs for dose escalation and variations of up-down designs, including two-stage designs combining simple strategies. The author uses logistic regression to model the unknown dose/response curve. Their discussion is in the context of estimating a maximum tolerable dose(MTD). Comparison criterion used is the fraction of patients treated above 50th-percentile, the resulting confidence intervals etc.
$\bullet$ J. O'QUIGLEY, M. PEPE AND L. FISHER(1990). Continual Reassessment Method: A Practical Design for Phase 1 Clinical Trials in Cancer. Biometrics, 46, 33-48.

The authors introduce a new approach, Continual Reassessment Method(CRM) to Phase I clinical trials. They use posterior distribution on model parameters to find the dose with posterior mean response (or response using posterior mean parameters) closest to the aimed-for target. They use parametric model for the dose-response curve with one unknown parameter, which Whitehead and Brunier (1995) argue is essentially equivalent to a logistic regression with slope fixed at 1.
[0.7mm] $\bullet$ S. N. GOODMAN, M. L. ZAHURAK, AND S. PIANTADOSI(1995). Some practical improvements in the continual reassessment method for phase I studies. Statistics and Medicine, 15;14(11):1149-61.

The Continual Reassessment Method (CRM) is a Bayesian phase I design whose purpose is to estimate the maximum tolerated dose of a drug that will be used in subsequent phase II and III studies. Its acceptance has been hindered by the greater duration of CRM designs compared to standard methods, as well as by concerns with excessive experimentation at high dosage levels, and with more frequent and severe toxicity. This paper presents the results of a simulation study in which one assigns more than one subject at a time to each dose level, and each dose increase is limited to one level. It is argued that these modifications address all of the most serious criticisms of the CRM, reducing the duration of the trial by 50-67 per cent, reducing toxicity incidence by 20-35 per cent, and lowering toxicity severity. These are achieved with minimal effects on accuracy.
[0.7mm] $\bullet$ E. L. KORN, D. MIDTHUNE, T. T. CHEN, L. V. RUBINSTEIN, M. C. CHRISTIAN, R. M. SIMON(1994). A comparison of two phase I trial designs. Statistics and Medicine, 13(18):1799-1806.

Phase I cancer chemotherapy trials are designed to determine rapidly the maximum tolerated dose of a new agent for further study. The authors argue that the previous comparisons of the continual reassessment method, a Bayesian method suggested to offer an improvement over the standard design, with the standard method did not completely address the relative performance of the designs as they would be used in practice. They conclude from their results that with the continual reassessment method, more patients will be treated at very high doses and the trials will take longer to complete, and offer some suggested improvements to both the standard design and the Bayesian method.
[0.7mm] $\bullet$ D. FARIES(1994). Practical modifications of the continual reassessment method for phase I cancer clinical trials. J Biopharm Stat.,4(2):147-64.

The continual reassessment method (CRM) for phase I cancer trials provides improved estimation of the maximum tolerated dose (MTD), and fewer patients receive ineffective dose levels compared to the traditionally used design. However, the CRM has not gained acceptance in practice owing to concerns with administering dose levels that
ISBA Newsletter, December 1999 BIBLIOGRAPHY

are too toxic. In this article, several conservative modifications of the CRM are introduced. The result is a procedure that improves estimation of the MTD and decreases the use of ineffective doses, without significantly increasing the use of toxic dose levels. The CRM with modification outperforms the traditional method in a simulation study.
$\bullet$ J.WHITEHEAD AND H. BRUNIER (1995). Bayesian decision procedures for dose determining experiments. Statistics in Medicine, 14, 885-893, Discussion 895-899.

This paper describes the Bayesian decision procedure and illustrates the methodology through an application to dose determination in early phase clinical trials. The situation considered is quite specific: a fixed number of patients are available, to be treated one at a time, with the choice of dose for any patient requiring knowledge of the responses of all previous patients. A continuous range of possible doses is available. The prior beliefs about the dose-response relationship are of a particular form and the gain from investigation is measured in terms of statistical information gathered. How all of these specifications may be varied is discussed. A comparison with the continual reassessment method is made.
[0.7mm] $\bullet$ J. O'QUIGLEY AND L. Z. SHEN(1996). Continual reassessment method: a likelihood approach. Biometrics, 52(2):673-84.

The continual reassessment method as described by O'Quigley, Pepe, and Fisher (1990) leans to a large extent upon a Bayesian methodology. Initial experimentation and sequential updating are carried out in a natural way within the context of a Bayesian framework. In this paper it is argued that such a framework is easily changed to a more classic one leaning upon likelihood theory. The essential features of the continual reassessment method remain unchanged. In particular, large sample properties are the same unless the prior is degenerate. For small samples and as far as the final recommended dose level is concerned, simulations indicate that there is not much to choose between a likelihood approach and a Bayesian one. However, for in-trial allocation of dose levels to patients, there are some differences and these are discussed. In contrast to the Bayesian approach, a likelihood one requires some extra effort to get off the ground. This is because the likelihood equation has no solution until a toxicity is observed. They suggest working initially with either a standard Up-and-Down scheme or standard continual reassessment method until toxicity is observed and then switching to the new scheme.
[0.7mm] $\bullet$ S. PIANTADOSI AND G. LIU(1996). Improved designs for dose escalation studies using pharmacokinetic measurements. Statistics and Medicine,15(15):1605-1618.

The authors describe a method for incorporating pharmacokinetic (PK) data into dose escalation clinical trial designs, to improve the efficiency and accuracy of these studies. The method proposed uses a parametric dose response function that models the probability of response in each person with two effects: the dose of drug administered and an ancillary pharmacokinetic measurements. After treatment and observation of each subject (or group of subjects) for response, one calculates the dose to be administered to the next individual (or group) to yield the target probability of response from the current best estimate of the dose-response curve. This procedure is a variant of the continual reassessment method (CRM). Statistical simulations employing a logistic dose-response model, dose of drug, and the area under the time-concentration curve (AUC) are used to demonstrate that the addition of pharmacokinetic information to the CRM is a practical and useful way to improve both dose-response modeling and the design of dose escalation studies.
$\bullet$ S. PIANTADOSI, J. D. FISHER, S. GROSSMAN(1998). Practical implementation of a modified continual reassessment method for dose-finding trials. Cancer Chemother Pharmacol, 41(6):429-436.

A practical, reliable, efficient dose-finding design for cytotoxic drugs applied in a multi-institutional setting is proposed. The continual reassessment method (CRM) was modified for use in phase I
ISBA Newsletter, December 1999 BIBLIOGRAPHY

trials conducted through the New Approaches to Brain Tumor Therapy (NABTT) Consortium. The implementation of the CRM in the paper uses (1) a simple dose-toxicity model to guide data interpolation, (2) groups of three patients to minimize calculations and stabilize estimates, (3) investigators' clinical knowledge or opinion in the form of data to make the process easier to understand, and (4) a flexible computer program and interface to facilitate calculations. The modified CRM was used in two dose-finding trials of 9-aminocamptothecin in patients with newly diagnosed and recurrent glioblastoma who were taking anticonvulsant medication. The CRM located the MTD efficiently in both trials. Compared to conventional designs, the CRM required slightly more than half the number of patients expected, did not greatly overshoot the MTD (i.e. no patients were treated at dangerously high doses), and did not underestimate the MTD. The authors conclude that their experience demonstrates the feasibility of implementing this design in multi-institutional trials and the possibility of performing dose-finding studies that require fewer patients than conventional methods.
[0.7mm] $\bullet$ J. WHITEHEAD AND D. WILLIAMSON(1998). Bayesian decision procedures based on logistic regression models for dose-finding studies. Journal of Biopharmaceutical Statistics, 8, 445-467.

Dose finding studies in cancer therapy are presented using logistic regression as d/r curve for the probability of adverse event. They consider a variety of loss functions and priors and use the utility at the MAP parameter values to approximate expected utility. For simulation purposes they use fixed sample sizes of 30 patients. They assume immediate observation soon after the drug has been administered. In the simulation they consider estimated dose and parameters and the percentage of dose allocations for each dose.
[0.7mm] $\bullet$ P. F. THALL AND K. E. RUSSELL (1998). A Strategy for Dose-Finding and Safety Monitoring Based on Efficacy and Adverse Outcomes in Phase I/II Clinical Trials., Biometrics, 54:251-264.

A non-decision-theoretic Bayesian strategy for dose-finding in clinical trials is proposed. The authors utilize a three-parameter proportional odds model that specifies the probabilities of both response and toxicity as functions of dose. Their algorithm selects doses for successive cohorts of patients based on maximum Pr(toxicity) and minimum Pr(response) limits initially elicited from the physicians. Design parameters are calibrated by simulating the trial under an array of clinical scenarios, with each scenario characterized by the probabilities of toxicity and response at each dose, and examining the (frequentist) operating characteristics of each parameterization.
[0.7mm] $\bullet$ P.F.THALL, E. H. ESTEY AND H. G. SUNG (1999). A new statistical method for dose-finding based on efficacy and toxicity in early phase clinical trials. Investigational New Drugs, in press.

The authors apply an extended version of the Thall-Russell (1998) design to a trial of donor lymphocyte infusion (DLI) as salvage therapy for acute myelogenous leukemia patients who are chemo-refractory. The extension provides a rule for choosing between two or more "best" doses that have clinically equivalent response rates. A simulation study is presented that compares the method, in the context of the DLI trial, to the continual reassessment method (O'Quigley, et al., 1990) and to the conventional method commonly used in most phase I chemotherapy trials. The simulation results indicate that the Thall-Russell method is superior, in part because the other two methods are based on toxicity alone and ignore response.
[0.7mm] $\bullet$ BERRY, D., M¨ULLER, P., GRIEVE, A.P., SMITH, M., PARKE, T., BLAZEK, R., MITCHARD, N., AND KRAMS, M. (1999). Adaptive Bayesian Designs for Dose-Ranging Drug Trials, in Case Studies in Bayesian Statistics 5 (C. Gatsonis etc. eds.).

Berry et al. use a Bayesian decision theoretic approach to dose-finding in a phase II clinical trial. Central to the proposed solution is a flexible probability model for the unknown dose/response curve which allows efficient analytic
ISBA Newsletter, December 1999 BIBLIOGRAPHY / PORTUGAL

posterior updating using a normal dynamic linear model (NDLM). Berry et al. split the decision problem into two steps: stopping (i.e., stopping the dose-finding trial vs. continuation) and dose allocation (in the case of continuation). Optimal stopping is solved as a formal sequential decision problem using an approximate numerical solution. The dose allocation problem is solved by choosing that dose which minimizes expected posterior variance of some key parameters of the unknown dose/response curve.

SOFTWARE

228 Phase I/II dose-finding, by Peter F.Thall, obtainable via anonymous ftp to ftp.odin.mdacc.tmc.edu.
228 Continual Reassessment Method, by Peter F.Thall,
$\bullet$ (source code)
/pub/source/crm-1.0.tar.gz
$\bullet$ (PC version)
/pub/msdos/crm-1.0-W32.exe
228 Modified CRM, by Steven Piantadosi, obtainable from the author: Spiantad@jhmi.edu

We would like to hear from readers on topics that they would like to see covered in this section. Please send your suggestions.

The first person in Portugal who showed interest in Bayesian Statistics and taught it at the University was Bento Murteira, a former professor at the School of Economics of the Technical University of Lisbon. In 1952 he introduced a modern course on Mathematical Statistics and Econometrics and later in the fifties he introduced, for the first time in Portugal, a course on Decision Theory. Although he had wonderful lecture notes that he used to give to his students, only in 1988 he decided he had improved them enough to have them published as a book, naming it Statistics: Inference and Decision. He published several papers on the application of Bayesian Statistics to economic data. He is now 75 years old and still very active and more and more interested in Bayesian Statistics. Nowhere else in Portugal, as far as we know, Bayesian arguments were taught till the early eighties. We can safely say that he has been our mentor and the force behind us.

Now it is time to say who ``we'' are, the Portuguese Bayesian group, and how we started and grew.

In the seventies, Statistics was already well established in the Faculty of Sciences in Lisbon, thanks to Tiago de Oliveira, but Bayesian methodology was considered just another ``crazy'' idea. Nevertheless he enthusiastically suggested Antónia Turkman to go ahead and study Bayesian Statistics. She went to Sheffield and in 1980 she finished her Ph.D. under the supervision of Ian Dunsmore.

Antónia came back to Lisbon to the Department of Statistics and Operations Research of the Faculty of Sciences full of ideas to spread the Bayesian spirit. It is not necessary to say how difficult the task was. Shyly she started teaching topics of Bayesian Statistics in the recently created M.Sc. course in Probability and Statistics. Daniel Paulino was one of her students who immediately caught the ``spirit'' and bravely decided to write his Master thesis on Regression Analysis under a Bayesian Perspective. We can say that this was the start. Daniel later went to São Paulo, Brazil and under the supervision of Carlos Pereira he finished his Ph.D. thesis on Analysis of Incomplete Categorical Data: Foundations, Methods and Applications in 1989.

When Daniel returned to Lisbon to the Department of Mathematics of the School of Engineering of the Technical University, he resumed his collaboration with Antónia who was still struggling in the Faculty of Sciences to convince people how nice the Bayesian Methodology was. In 1992 her first Ph.D. student, João Pedro Faria defended his thesis on Subjective Probability, entering into the small family of Bayesians, who were still seen as ``extravagant statisticians''. Meanwhile, Antónia and Daniel in their teaching activity continued to spread Bayesian
ISBA Newsletter, December 1999 PORTUGAL

ideas and methods even to an undergraduate audience and to supervise students at the M.Sc. and Ph.D. levels forming the core of what is now the Bayesian group in Portugal.

Categorical data and Missing values (Daniel Paulino and his Ph.D. student Paulo Soares);

Survival models with frailty (Antónia Turkman and his Ph.D. student Giovani Silva);

Time series analysis (Isabel Pereira, a former Ph.D. student of Antónia Turkman);

Prediction in errors in variables models (Fernando Magalhães, who also took his Ph. D. in Sheffield in 1997 under the supervision of Ian Dunsmore, and his Ph.D. student Maria João Polidoro);

Screening methods in environmental health (Antónia Turkman and her Ph.D. student Natércia Durão);

Bayesian methodology applied to extremes (Patrícia Bermudez, Feridun Turkman and Antónia Turkman).

This group, however small, has been very active inside the Portuguese Statistical Society, namely being members of the directive board, organising some of the Society Annual Conferences, and bringing to these conferences renowned Bayesian statisticians as invited speakers.

There are also researchers, outside the University, who show interest in the application of Bayesian methods and very often join the group for seminars, courses, conferences, and so on. We would like to mention a marine biologist, Manuela Azevedo, who works in Fisheries and has been very active in the spread of Bayesian ideas in her scientific community. She was a co-organizer of a section on Bayesian Methodology applied to Fisheries in the ICES Annual Science Conference, which recently took place in Stockholm. Also we want to mention Paulo Nogueira, a Public Health researcher, and Luzia Gonçalves, a statistician who has showed interest in the application of Bayesian methods in genetics.

Besides this group in Portugal we know of the following Ph.D. students abroad who are working on Bayesian Statistics: Sofia Dias (University of Sheffield), Rui Paulo (Duke University) and Bruno Sousa (Michigan University ) and who hopefully will come back to Portugal to increase the population of Bayesian statisticians and to broaden the field of Bayesian research in Portugal.

The growing interest in Bayesian methods among statisticians and other researchers led us to organise in February 1999 an open intensive course on Bayesian Statistics with special emphasis on applications. This course was lectured by Bento Murteira, Antónia Turkman, Daniel Paulino and João Faria. Tutorials using Bayesian packages were given by Giovani Silva, Paulo Soares and Patrícia Bermudez. The success of this course was such that a similar one will take place in the year 2000. Meanwhile, as a result of the course, the lecture notes were greatly improved and are being organised as a book on Bayesian Statistics (in Portuguese) which is due to appear soon.

ISBA/SBSS ARCHIVE FOR ABSTRACTS

All authors of statistics papers and speakers giving conference presentations with substantial Bayesian content should consider submitting an abstract of the paper or talk to the ISBA/SBSS Bayesian Abstract Archive. Links to e-prints are encouraged. To submit an abstract, or to search existing abstracts by author, title, or keywords, follow the instructions at the abstract's web site,

www.isds.duke.edu/isba-sbss/

The Bayes Linear Programming Language [B/D] (an acronym for BELIEFS ADJUSTED by DATA) is an interactive language developed by David Wooff and Michael Goldstein which allows complete prior/posterior analysis and consistency checks of Bayes linear statistical problems. The Bayes linear approach is concerned with situations in which prior judgments are combined with observational data through the use of expectation, rather than probability. Therefore, the methods can be of particular relevance in complex problems with too many sources of information and that do not require the level of detail of a complete Bayesian analysis.

[B/D] is an environment that permits the user to specify prior beliefs on quantities of interest only through expectation and covariance. The update of beliefs through data is obtained via adjusted means and variances. An adjusted mean or a Bayes linear expectation is the linear combination of the data that minimizes the mean square error to estimate individual quantities. An adjusted variance is the variance of the quantity of interest minus its Bayes linear expectation. For the usual Bayesian approach, adjusted expectation offers a simple approximation to conditional expectation, while adjusted variance is an upper bound to expected posterior variances over all consistent prior specifications with the defined structure. The approximations are exact in some important cases, particularly when the joint probability distribution of the quantities of interest and data follows a multivariate normal.

Different checks are included to study consistency between the data and prior beliefs. [B/D] permits the calculation of canonical directions and its resolutions. These canonical variables are uncorrelated linear combinations of the quantities of interest that detect directions in which adjustments by the data are more informative. Additionally, [B/D] constructs the bearing which is the linear combination of the quantities of interest that measures the magnitude of the adjustment in belief.

The software also provides interactive influence diagrams to summarize graphically the Bayes linear adjustments. These diagrams may be firstly used to represent the qualitative form of the covariance structure between the components of the problem and, secondly, to give a simple graphical representation of mean/variance adjustments jointly with consistency checks based on canonical variables and bearing. Also, [B/D] considers adjustment of beliefs by stages, which assists the user in studying the impact of different sources of information in the Bayes linear methodology.

The language runs on DOS, Windows and Unix. Available versions on the web are for a 386/486/Pentium PC running Microsoft Windows Version 3.1 or later and for Linux which has been tested on a PC with 32MB in RAM. The Windows version is limited to construction of beliefs of up to 100 random quantities, and to the adjustment of up to 100 random quantities with a second stage of up to 100 others. Furthermore, the Linux version allows up to 500 random quantities to assess beliefs, and to the adjustment of 250 random quantities by up to 250 others. Versions are supplied for machines with or without a co-processor. Versions of smaller and larger sizes, or working under SUN workstations, are available under request from the authors. The zipped version of the program files needs about 440K disk space which expand into 1.3MB. The postscript documentation is about 800K and expands to 2.4MB.

The [B/D] language, the reference manual (both html and postscript formats) and all other related documentation are freely available to the academic community and for non-commercial purposes at

or from the STATLIB archive at Carnegie Mellon University.
ISBA Newsletter, December 1999 STUDENT'S CORNER

It has been my great pleasure and a fantastic learning experience to have served as the Associate editor of the new ISBA newsletter's Student's Corner. It gave me the opportunity to interact with a lot of fellow graduate students in different universities who were in the heart of writing their thesis. On a more selfish note, not only did this interaction educate me on the current research activities, it also helped me learn the style and organisation behind writing a thesis. I am now tring to apply some of these techniques that I learned as I am in the process of constructing my own thesis.

When Fabrizio first asked me to take up this job, I was rather apprehensive about it since I had no experience at all in editorial work. However, Fabrizio really turned out to be a ``cool customer'' who never panicked. He gave me clear directions as how to proceed with the work, introduced me to the people I need to contact and guided me on how to organise the material. Fabrizio himself is at the very heart of the newsletter and it was because of his tireless efforts that we could bring out the Student's Corner.

While the main objective of the Student's Corner has been to present abstracts of dissertations that are underway at various distinguished institutes that are engaged in Statistical (in particular Bayesian) research, it was also hoped that the section would serve as a platform for students to interact. This latter hope has not been fully realized until now. It is our hope that the section would generate constructive discussions based upon the abstracts and research projects that are published in the Section. We would also like students to present problems that they have encountered (and perhaps solved) in their research.

Once again, I would like to thank Fabrizio for this wonderful opportunity and learning experience and wish the Newsletter a very prosperous future.

1999 Ph.D's at
ISDS, Duke University

(Dissertations available at
www.isds.duke.edu/people/
alumni.html)

Jacob Laading
jacob@nr.no
Practical methodology for inclusion of modality-specific modifications in a hierarchical Bayesian deformation model
Advisor: Valen Johnson

distributions can be obtained in closed form. This allows quick implementation of the model, and provides full probabilistic inference for the parameters, interpolations, and forecasts. To illustrate the method, I analyze two large datasets: one involving tropical rainfall levels and the other Atlantic ocean temperatures.

In the second essay, I propose a new Markov chain Monte Carlo (MCMC) smoother for nonlinear, non-Gaussian state-space models. The method can be used to conduct posterior inference in a broad class of dynamic models. The key idea is to construct an approximate state-space model based on mixtures of normals. This approximation is then used to define the proposal distribution in an efficient Metropolis-Hastings MCMC algorithm, which provides samples from the posterior distribution. To illustrate the method, I consider three simulated examples: an exponential observation model, a stochastic volatility model, and a popular nonstationary growth model.

In the third essay, I propose a simulation-based approach to decision theoretic optimal Bayesian design in the context of population pharmacokinetic (PK) models. Depending on the application, these models are also known as repeated measurement models, random effects regression models, longitudinal data models, or population models. I consider the problem of choosing sampling time for the anticancer agent paclitaxel (Taxol), using criteria related to total area under the curve (AUC), time above a critical threshold, and sampling cost.

We are pleased to announce that partial travel support is available for a limited number of statisticians from developing countries and young investigators who are planning to present their research work at ISBA 2000. Note that the deadline for submission of abstracts in final form was December 31, 1999.

A young investigator is anyone whose Ph.D. (or equivalent academic degree) was completed no earlier than December, 1993, or who is currently working on his/her doctoral dissertation. Young investigators from all countries will be eligible for support.

The application form can be obtained at:
www.bayesian.org/ isba2000/form_trav2.html

228 Key Dates.
$\bullet$ January, 31st, 2000:
Deadline for registration at the prices in the registration form
$\bullet$ February, 15th, 2000:
Confirmation of registration and hotel reservation

228 Contact.
$\bullet$ Conference Co-Chairs

Philip Dawid <dawid@stats.ucl.ac.uk>
Photis Nanopoulos <photis.nanopoulos@eurostat.cec.be>

$\bullet$ Scientific Committee Chair

Mike West
<mw@stat.duke.edu>

$\bullet$ Finance Committee Co-Chairs

Alicia Carriquiry <alicia@iastate.edu>
Steve Fienberg <fienberg@stat.cmu.edu>

$\bullet$ Local Organising Committee Chair ISBA Newsletter, December 1999 NEWS FROM THE WORLD

228 Internet Resources

Debug's searchable article database. The German BUGS User Group ``debug'' offers now free online search in a database of statistical articles, both in German and in English. The focus is on topics related to MCMC, hierarchical and graphical models. You can also add entries to the database. See under http://userpage.ukbf. fu-berlin.de/~debug/

History of mathematics. Life is good for only two things, discovering mathematics and teaching mathematics (S. Poisson). Find this apodictic quotation and a lot of other information on mathematics at the ``MacTutor History of Mathematics archive'' (http:// www-history.mcs.st-and. ac.uk/~history/index.html), featuring, among many things, history of mathematics, mathematicians' biographies (Bayes's is covered), and an index of famous curves (with graphics). All sections are searchable.

228 Job Opportunities

Jobs in Statistics. A list of links related to jobs in Statistics (mainly in the United States) can be found at http://www-stat. ucdavis.edu/jobs.html. It includes links to job boards (like the one at University of Florida, http://www.stat.ufl.edu/vlib/ jobs.html), searchable job archives, other lists of links ...

HSSS and Parallel Architecture. The Department of Statistics, Trinity College Dublin, has a 30 month postdoctoral position to work in the area of so-called highly structured stochastic systems. The position is available from April 2000.

The project is under the supervision of Simon Wilson (simon.wilson@tcd.ie) and John Haslett (john.haslett@tcd.ie) and is part of Trinity College's High Performance Computing initiative, a collection of research projects in science, engineering and mathematics based around a 48 node IBM supercomputer.

The aims of this position are to investigate methods of exploiting parallel algorithms in MCMC methods. The particular application in mind is spatial Gaussian models and modelling of the so-called ecological fallacy. More generally, we would like to investigate the suitability of implementing MCMC with common highly structured stochastic systems using parallel architectures, such as hierarchical, multi-resolution, 3d field, spatial Gaussian, etc. Finally, in the light of the experience gained with working on the
ISBA Newsletter, December 1999 NEWS FROM THE WORLD

above, we would like to draw conclusions on the performance of various MCMC approaches, that is a meta-analysis of the huge ``Tower of Babel'' of MCMC techniques now available.

pounds (about 25,400 Euro), rising to 21,000 Irish pounds in the second year and the equivalent of 22,000 Irish pounds per year in the final 6 months.

228 Miscellanea

1999 ICES Annual Conference. Report by R. Conser and M. Azevedo. In 1999, the Annual Conference of the International Council for the Exploration of the Sea (ICES) took place in Stockolm, Sweden, from 29 September to 2 October. One of the theme sessions was on Bayesian Statistics (see the announcement on the ISBA Newsletter, vol. 6, No. 2).

Bayesian approaches applied to fisheries analysis have become quite common in the fisheries literature - more than 100 papers have been published over the past decade. While Bayesian approaches have been applied for some stock assessment work within ICES working groups (at least two known cases), they have not been used commonly for stock assessment and for the provision of management advice in the ICES arena. The question of whether or not ICES should be moving more rapidly in this direction was posed by the co-conveners for the theme session consideration and discussion. Five papers were presented during this theme session; they provided an overview of the Bayesian approach as applied to fisheries research problems, demonstrated applications for stock-recruitment modelling, and discussed a Bayesian-like procedure for assigning ages to eggs of synchronous spawning fish.

The general sense of the following discussion was that while the Bayesian approaches have significant conceptually advantages for fisheries analysis generally and for ICES assessments in particular, practical implementation difficulties may warrant a cautious strategy when advocating their increased usage among ICES assessment working groups. For example, the increased computational demands of these methods may not be practical within the current ICES working group framework. The added model complexity (over ICES status quo models) will require additional efforts to educate fishery managers so that assessment results can be readily and accurately communicated. The ICES experience has generally been that both quality control and the provision of management advice are made more difficult when complicated models and analyses are employed.

However, Bayesian approaches do provide a systematic means for better expressing uncertainty in ICES management advice. In particular, the potential to incorporate the uncertainty associated with structural model choices (in addition to parameter estimation uncertainly) is quite important, and is not fully accounted for in present ICES advice. In the short term, Bayesian approaches may be most useful in the ICES arena for addressing more focused research issues (e.g. the stock-recruitment work) rather than for stock assessments per se. But further research among ICES scientists and perhaps within the Assessment Methods Working Group is encouraged.

Evaluating research and development projects. The Statistics Group at the Universidad Nacional de Quilmes has a contract with the local Agency for Promotion of Science and Technology to develop a Bayesian MC-based expert system for the evaluation and monitoring of individual industrial R&D projects in Argentina. The Agency is the local counterpart of a loan from the Interamerican Development Bank of $ 200.000.000. The Group is also developing an expert system to detect the optimal portfolio out of a group of R&D projects, based on Bayesian estimation of parameters (posterior estimation during monitoring) and multicriteria nonlinear functions to find the Pareto-optimal solution. Most of the projects will be evaluated by peers with statistical tools and by political authorities on the basis of the peers' report and of political issues. Contact Alfredo Russo (arusso@unq.edu.ar) for further information.

93 ISBA's Vice Program Chair. Tony O'Hagan has accepted appointment as ISBA's Vice Program Chair for year 2000.

There are many benefits associated with joining the society not the least of which is the subscription to the ISBA Quarterly Newsletter. Please complete this form and return it with your membership fee to:

Professor Valen Johnson, ISBA Treasurer
Institute of Statistics & Decision Sciences
223 Old Chem Building
Box 90251
Duke University
Durham, NC USA 27708-0251
voice:(919)-684-8753
fax: (919)-684-8594
valen@stat.duke.edu
http://www.isds.duke.edu/~valen/

I wish to become a member of ISBA		I wish to renew my ISBA membership
$\bigcirc$ Regular rate (U.S. $ 25.00)	$\bigcirc$ Regular rate (U.S. $ 25.00)
$\bigcirc$ Reduced rate (U.S. $ 10.00) (*)	$\bigcirc$ Reduced rate (U.S. $ 10.00) (*)

Name

Institution/Company

Department

Street Address

City, State/Province

Country, ZIP/Postal Code

Phone Fax

E-mail

I want the information available for others: Yes $\bigcirc$ No $\bigcirc$

Membership fee (*) for 2000 is U.S. $25.00.

$\bigcirc$ Enclose check in U.S. $ payable to International Society for Bayesian Analysis

$\bigcirc$ Credit card payment

AmeExpress $\bigcirc$ MasterCard $\bigcirc$ VISA $\bigcirc$

Card # Exp.

Date Signature

(*) The membership fee for calendar year, Jan. 1 to Dec. 31, 2000 is U.S. $25.00. ISBA also has reduced rates for certain individuals. This reduced rate has been fixed at $10 for 2000 . People who can apply for that include students (full proof of status; maximum of 4 years in a row) and permanent residents of selected countries. A country qualifies for the reduced rate in 2000 if its GNP per capita based on the World Bank Data for 1996 is no greater than $6,000. For example, this includes the countries where our three current Chapters reside (Chile, India and South Africa). ISBA Newsletter, December 1999