THE ISBA NEWSLETTER
Vol. 6 No. 2 June 1999
The official newsletter of the International Society for Bayesian
Analysis
ELECTRONIC ARCHIVE
FOR ABSTRACTS
by Robert Wolpert
Editor, ISBA/SBSS Archive
rlw@stat.duke.edu
ISBA, in collaboration with the Section on Bayesian Statistical Sciences
of the American Statistical Association (SBSS of the ASA) has founded a
searchable Electronic Archive for abstracts of Bayesian papers and
conference presentations. The Archive is hosted by the Duke University
Institute of Statistics and Decision Sciences (ISDS).
All authors of statistics papers and speakers giving conference
presentations with substantial Bayesian content should consider
submitting an abstract of the paper or talk to the ISBA/SBSS Bayesian
Abstract Archive. Links to e-prints are encouraged. To submit an
abstract, or to search existing abstracts by author, title, or keywords,
follow the instructions at the abstract's web site,
www.isds.duke.edu/isba-sbss/
The archive is new and some problems may arise; please report
difficulties or suggestions to archive@isds.duke.edu. Conference
organizers are also encouraged to submit Bayesian session abstracts by
e-mail to the Abstract staff at the address above. Thank you.
A WORD FROM
THE EDITOR
by Fabrizio Ruggeri
ISBA Newsletter Editor
fabrizio@iami.mi.cnr.it
We are pleased to present you a new issue of the Newsletter.
As you will see, relevant ISBA activities, like ISBA 2000
(do not forget the October, 1st deadline!) and the Bayesian
archive, are presented along with various articles. As promised, ISBA
members (the only recipients of the current issue) are getting a
newsletter like a magazine: we will not
present theorems and zillions of MCMC runs, but e.g. ways of
spending cold, wet Saturday afternoons .... We continue our
series of interviews with Steve
Brooks, a young, well known researcher. If you want to suggest
someone to interview (even if not Bayesian!), please contact the
two Associate Editors. We are presenting two stimulating contributions
on teaching and applications, due, respectively, to Romano Scozzafava
and Mark Glickman. Two Associate Editors have reviewed, respectively,
papers on Bayesian methods in epidemiology and software for Model
Averaging. A relevant part of the Newsletter is devoted to present
research by recent Ph.D. recipients and candidates: this time we
focus on Carnegie Mellon and one of the Ph.D. programmes in Italy.
We continue
our tour among Bayesian communities worldwide by looking at what
happens in Greece, the location of the next ISBA conference. Finally,
we have a rich selection of news from the world, partly provided by
our Corresponding Editors and ISBA members.
Contents

ISBA Newsletter, June 1999 INTERVIEWS
STEVE BROOKS
by Michael Wiper
mwiper@est-econ.uc3m.es
Steve Brooks is one of the foremost workers in MCMC methodology today and is the administrator of the
MCMC preprint service (address at the end of the interview).
He took his PhD thesis in MCMC with Gareth Roberts at Cambridge and joined
Bristol University as a lecturer in 1996. He has recently won the 1999 Royal Statistical Society
research prize and will be
moving to the University of Surrey as a Senior Lecturer in August 1999.
We e-mailed Steve a number of questions about his career
and the Bayesian world in general. Here are his responses.
1) Why did you decide to become a statistician?
When I came to the end of my degree I was torn between all sorts
of careers. In a way this was the default choice, I was always
thinking, ``I'll just do another course, while I decide what I want
to do". I'd always enjoyed Maths and the sense of achievement
you got when you solved a difficult problem. I'd also been strongly attracted
towards working on something that could really make a difference in the
real world. Statistics seemed the obvious area, combining rigorous
mathematics with a strong emphasis on applications.
2) Who were/are your (statistical) heroes? And why?
I'm not sure I have heroes, but there certainly quite a few people
who have inspired me. One of my biggest influences has been Byron
Morgan. He was my MSc supervisor and then I worked with him as
a researcher for a year before my PhD. He always manages to ask
exactly the right question and we've done (and are continuing to do)
some great work together. There are others too, who have had a more
hands-off influence on me. People like Persi Diaconis, Bernard Silverman
and Adrian Smith. You can't help but admire people like them and hope
that one day someone might think of you in the same way.
3) You have worked in Bayesian computation and MCMC
from almost the start of your statistical career.
What are the most important developments you have seen?
Well I started in this area in 1993, I guess. Back then MCMC was in it's
infancy and there's been phenomenal growth over the past 6 years. Methodological
advances have to include things like reversible jump MCMC and perfect simulation,
which may potentially revolutionise our field. However, I think that these will
have less of an impact on the field over time than we might expect. Already we're
beginning to see alternative model-jumping algorithms to rival RJMCMC and perfect
simulation seems constrained to only a small class of problems at the moment.
Getting away from the methodology, I'd have to say that the BUGS project has had
an enormous impact, particularly in opening up the methodology to practitioners
who might not have the computational background to program these things
themselves. The introduction of ideas and, in particular, the notation
from graphical modelling has also been extremely influential. For example, the
expression of a complex statistical model in the form of a DAG seems such a natural
thing to do and makes the communication of ideas between statisticians and
practitioners so much easier.
4) What do you think will be the next major developments in Bayesian computation?
I can't help thinking that there's some grand sampling scheme out there somewhere and
that the algorithms we work with today are just different faces of some more general
approach. Of course I've no idea what that is, but I'd love to be the one who
sees it first... Also, adaptive MCMC is an area that's never really taken off. The idea
of developing algorithms that adapt themselves to the target distribution as the
simulation proceeds so as to improve mixing or other desirable properties. This seems
like such a natural idea, but there's been very little published work. I would see this
as an area with enormous potential.
And in Bayesian statistics more generally?
There's a lot of interest in financial stuff these days. Obviously there's
a lot of money in it, but there's some great
ISBA Newsletter, June 1999 INTERVIEWS
problems too. State space modelling
seems like a big area here, I like the sort of things that Mike West and
Neal Shepherd are doing. Spatial modelling is also a big area now that we have
the tools to model these processes properly. One major open problem, to me
at least, is a more philosophical one and what we should be doing with
our models. Should we choose models or average over them? Should we take an
M-open or M-closed view? There seems to be no agreement on these sorts of
questions and a great deal of work being done to try and develop a coherent
interpretation of the Bayesian philosophy to these sorts of questions. Just what
does a Bayesian believe about the model? Of course, we now have non-parametric
approaches too. Some see these as the way forward, but I'm pretty keen on
carefully choosing my model myself. I don't fancy trying to explain a non-parametric
approach to any of my Ecologist collaborators for example!
5)
How did the MCMC preprint service start? And for the few Bayesians who know nothing about it, what
is its purpose?
The idea was first proposed (I think) by Charlie Geyer. It was at one of the
Mt Holyoke meetings in 1994. The problem was that the area was
developing extremely rapidly
and the inevitable delay between submission of papers
and their publication often meant that papers were out of date
by the time they appeared. The idea of the service was to provide a
central location for papers on MCMC so as to keep the community up-to-date
on current developments.
Everyone agreed that it was a great idea but
nobody had the time to set it up. My PhD supervisor, Gareth Roberts, came back
from the meeting and mentioned the idea and I've never really looked back.
The basic idea of the service is to maintain a web-based list of preprints or technical
reports on MCMC methodology. People can access the site, search the database or
check for the latest additions and then download PostScript or PDF files of
papers that look interesting. There is also information on relevant conferences
and links to code for performing MCMC simulations etc,....
6) Would you like to see more work published on the Web, or do you prefer paper publications?
I must admit I'm a little old-fashioned and prefer to have nicely bound and
presented journals rather than whole piles of reprints on my shelves. I really
do like the idea of publishing preprints on the Web, though. I think it helps
the community grow faster. Of course, you do have to be a little careful; Web-based
material is rarely refereed and there has been the odd problem with papers
sent to the preprint list, for example.
7) What advice would you give to teachers of Bayesian statistics? How do you make
teaching MCMC simple?
I find it's much easier to learn if the students feel involved with a class. I like
using long stories and practical experiments to try help the students get to grips
with the concepts. At Bristol, I used to teach Bayesian statistics to third year
undergraduates, who had never come across the ideas before. So, it was important
to try and put the Bayesian ideas across within the frequentist world in which
they'd been brought up. One of my favourite ways of doing this is to tell them the
following story. ``Suppose you're relaxing in your favourite chair early one
morning and staring out of the window across your front lawn. Your eye
casually falls on a large object in the middle of the lawn. It looks like a
large and
long pole standing upright with lots of small green bits hanging off of what look like
brown arms. As it
gently sways in the breeze you entertain two possibilities; either it is a tree
or a mailman. Of course you decide it must be a tree because the likelihood of it being
a tree, given the description is considerably higher than than that for a mailman.
Now suppose you entertain a third possibility; perhaps it's a fake tree. Now, the
likelihood tells you nothing and you can't decide between it being a tree or
a fake tree. However, a priori you know it's unlikely that someone will
have placed a fake tree in your garden and by combining this knowledge with
the likelihood, you are able to identify the object as a tree." As I work through
this story, I assign letters to the different events and write probability
ISBA Newsletter, June 1999 INTERVIEWS
statements on the board. The idea is to walk them through a simple example with
intuitively obvious steps to make the whole idea seem more familiar to them. Most
of them realise that they were Bayesians all along, they just didn't know it!
MCMC can be taught similarly. One example I use here is to arrange the class
in rows. The person on the left-hand end tosses a coin and passes it to the
person to their right.
This person then tosses two more coins. This person now has three coins and
there must be either more Heads or Tails. This person passes to their right
one of the coins which shows the side which appears most of the three before them.
The next person tosses two coins and looks at those two, together with the
one from their left etc,... This simulates a Markov chain, and by starting
all of the chains of with Head for example, you can explain the ideas of
starting point bias, convergence etc,.... You can then go through the maths and
prove that the chain has a stationary distribution putting equal
probability on Heads and Tails.
Ideas like this help the students to engage with the ideas and to think
about them again outside of class. It's also fun!
8) Have you ever had any amusing (Bayes) questions or comments from students in your
stats classes?
A few months ago I had a very annoyed student come into my class. She'd been sitting
in her car trying to decide whether or not she should buy a parking
ticket for 2 pounds or risk a fine of 15 pounds if she were caught without one.
The day before, we had gone through a few decision theory problems and she
decided to choose the option which minimised her expected loss and didn't
buy a ticket. Unfortunately, her prior on the arrival rate of traffic wardens
was a bit off and she was fined. She seemed to think the whole thing was my fault!
9) What do you enjoy most about your work?
It's got to be the people. Bayesians in particular seem to be such nice people,
just look at the conferences! Of course, I enjoy positive feedback. I've written a
couple of review papers in the past few years and it's great to hear
people have been reading them, using them for discussion groups etc,...
It's a great feeling to know that all the effort it took to put pen
to paper was worthwhile and that someone out there appreciates it.
And least?
Actually, there's not a lot I don't like about the job. I guess the statistical
community, as it becomes more strongly market driven, is much more
competitive than it used to be. I find myself watching what I say at
conferences a little and trying to not to give my best ideas away before I've
had a chance to work on them myself. I've been stung that way a couple of
times now, and it saddens me that some people are willing to steal ideas from
others. Perhaps it's always been that way, but I always used to have the
impression that academics were better than that.
10) What is your favourite statistics book?
I love books, I always have. I probably have around 200 statistics books
on my shelves. I guess my favourite book should be the one with the cover
most worn, that would probably be Feller ``An Introduction to Probability
Theory and Applications". However, there are loads of other great books
out there. My favourites would have to include Carlin and Louis (Chapman and
Hall, 1996); Gelman, Carlin, Stern and Rubin (Chapman and Hall, 1995);
Robert (Springer, 1994) and,
for teaching, I love Gamerman's book on MCMC.
11) What is your favourite Bayesian statistics joke?
I haven't heard many, but one comment that tickled me recently was when we were
on a beach at a recent conference. We had decided to go for a swim and as
we were running off, someone shouted ``last one in's a frequentist!". It wasn't even
a Bayesian conference, but the idea just made me laugh.
As a member of ISBA, what if any changes would you like to see in the Society?
That's hard. I think the idea of an independent conference every four years
spaced between the Valencia meeting is a great one and I hope the first one
in Crete next year is a great success.
I guess it might be nice to see ISBA
working on both the national and international level. For example, ISBA
is often
ISBA Newsletter, June 1999 INTERVIEWS / SOFTWARE
associated with major international conferences, but at the national
level, only with the JSM. Perhaps we could think about how we can operate
more efficiently on the national level by having a presence at national conferences
outside the US, like the annual RSS conferences in the UK for example.
Thanks to Steve for a very interesting interview.
The MCMC preprint service is at
http://bris.ac.uk/MCMC/. The homepage of the Bugs project is
www.mrc-bsu.cam.ac.uk/
bugs/Welcome.html.
The books Steve mentioned are
Carlin, B. and Louis, T. (1996). Bayes and Empirical Bayes Methods for Data Analysis, Chapman and
Hall.
Gelman, A., Carlin, J., Stern, H. & Rubin, D. (1995). Bayesian Data Analysis, Chapman and Hall.
Robert, C. (1994) The Bayesian Choice, Springer.
Gamerman, D. (1997) Markov Chain Monte Carlo, Chapman and Hall.
BAYESIAN MODEL AVERAGING SOFTWARE
by Gabriel Huerta
gabriel@bayes.stats.nwu.edu
We review software by Raftery, Volinsky and Hoeting.
This software provides S-Plus code that implements Bayesian
Model Averaging (BMA) to account for model uncertainty in many
statistical models including linear regression, generalized linear
models and Cox's proportional hazard models. The S-Plus functions:
bic.glm, bic.surv, bicreg and bic.logit written
by A. Raftery and C. Volinsky solve the variable selection
problem by averaging over the best models according to posterior model
probabilities. The function bic.glm (Volinsky) implements the model
averaging for a large class of generalized linear models as defined by
the S-Plus function glm. Choices include: Gaussian, Poisson, Gamma,
Inverse Gaussian and Binomial distributions. For survival analysis, the
function bic.surv (Volinsky) implements the BMA for Cox's proportional
hazard model. Additionally, the functions bicreg (Raftery) and bic.logit (Raftery) implement model uncertainty for
a standard linear regression and a logistic regression
respectively. The marginal likelihoods used to compute the posterior
probabilities are obtained with the BIC approximation and consequently does
not involve a specific prior for the parameters of each model that is averaged.
The exploration of the model space follows the principle of Occam's razor
or principle of parsimony for scientific explanation. Initially, a leaps and bounds algorithm is performed to produce some candidate or ``top''
models. When more than 30 independent columns are specified, the S-functions
reduce to 30 regressors using a backward elimination procedure. Then, Occam's window is built to only consider those models that have, at least,
a posterior probability equal to 1/C of the maximum posterior probability
for all models; C a value that can be fixed by the user. As an option to the
user, the model space may be restricted to eliminate those models that receive
less support from the data than some of its sub-models in terms of posterior
probability.
In broad terms, the input for the S-Plus functions are vectors, matrices or
scalars that define the response variable, the independent variables, the prior
probabilities for models, indicators
for censored or uncensored data, when appropriate, and specifications for the
leaps and bounds and Occam's window steps. The output produces a list of
objects that include the posterior probabilities, approximated BIC's,
deviances and degrees of freedom for the selected models. Also, it contains
the maximum
likelihood estimator of each regression coefficient for each selected model,
the posterior mean of the coefficients averaged across models and their
posterior standard deviations.
Furthermore, the function glib written by A. Raftery, carries out
Bayesian estimation, model comparison and accounts for model uncertainty in
generalized linear models, notably logistic regression and log-linear
models. It differs from the other S-functions in two aspects
mainly. It does not use the BIC approximation but
ISBA Newsletter, June 1999 SOFTWARE / ISBA 2000
carries the Bayesian analysis using a reference set of
prior distributions that involve Normal forms. Also, it does not use Occam's
window or the bounds
and steps algorithm and rather requires that the user specifies all the
models to be considered. The output for this function contain lists
that have model comparison results, the
posterior probabilities for models, posterior means and
posterior standard deviations for parameters averaged across models.
Also, the software includes a collection of S-Plus programs that performs
Bayesian simultaneous variable selection and outlier identification
(SVO) via Markov Chain Monte Carlo model composition (MC3) for a
linear regression. The programs are known as BMA.shar and were written
by J. Hoeting. The model allows for mixtures of normal errors with a variance
that may be inflated by a scalar factor specified by the user. The priors used
for model coefficients and variance are the standard Normal-Gamma conjugate
distributions. The basic idea for MC3 is to explore the model space
with Metropolis-Hastings steps where candidate models are proposed
within a neighborhood of the current model. The neighborhood is
usually defined with either one predictor more or one outlier more or
with one predictor less or one outlier less. The inputs of the main
function MC3.REG involve the response variable, the matrix of
all possible covariables, number of iterations for the MCMC, an
initial or candidate model, a list of potential outlying observations,
a parameter indicating the probability that a particular observation is an
outlier and the inflation factor for the error variance. As output, the
program returns a matrix that has information on the selected models visited
at each MCMC, a list of outlying observation for each visited model, the number
of times the model was visited and the posterior model probabilities.
All these S-functions can be freely used and freely distributed for
non-commercial purposes only and downloaded from
www.research.att.com
/~volinsky/bma.html
Questions about this software should be addressed to the authors (see their addresses
in the above web page.
Call for session organisers and papers
ISBA 2000
The 6th World Meeting of the International Society for Bayesian Analysis
Hersonissos, Crete
May 28-June 1 2000
We expect to publish many of the theme papers in a special issue
of the EUROSTAT journal, ``Research in Official Statistics.''
Full details of the plan and schedule will be announced shortly.
We remind that proposals for sessions or for individual talks must be
received by Mike West < mw@stat.duke.edu> (Committee Chair) no
later than October 1, 1999. More details are available at the ISBA
web site www.bayesian.org and in the March issue of the ISBA
Newsletter.
ISBA Newsletter, June 1999 TEACHING
A CONTRIBUTION
by Romano Scozzafava
romscozz@dmmm.uniroma1.it
Are the Frequentist and Bayes Approaches in Conflict?
I feel that a question such as ``Is it desirable to teach both
Bayesian and frequentist thinking in an introductory class?" is, in a sense,
misleading. In fact (as I stress in my teaching in the Engineering Faculty
of ``La Sapienza" in Rome) the subjective view of probability is not in
contrast with a frequentist (or else a
combinatorial, i.e. classical) approach, since the latter can be seen just as
particular ``methods of evaluation" of a probability. This merged approach
easily overcomes barriers created by the usual prevailing opinions, giving up
any artful limitation to
particular events (such as ``repeatable" or ``symmetric", not even clearly
definable). An event E is just any unambiguous proposition that can only
assume two ``values", 1 or 0 (regarding it as a simple random variable). The
lack of information on the actual value of E easily paves the way to the
introduction, as an ``ersatz", of the concept of
probability: a value p = P(E) is regarded as an amount to be paid to bet
on E, with the proviso of winning a unit amount of money if E occurs and
nothing if E does not
occur. Then coherence is introduced by the requirement that the choice of
p would not make the player a sure loser or winner. If E is different
from 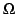 and
and 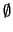 (certain and impossible events), the two
possible ``gains" are
G(E) = - p + 1 (if E occurs),
G(Ec) = - p (if E
does not occur), and so, since coherence requires that they must not be both
negative or both positive, p must satisfy
- p(1 - p) < 0, which is the
same as 0 < p < 1 . On the other hand, when
E =
(certain and impossible events), the two
possible ``gains" are
G(E) = - p + 1 (if E occurs),
G(Ec) = - p (if E
does not occur), and so, since coherence requires that they must not be both
negative or both positive, p must satisfy
- p(1 - p) < 0, which is the
same as 0 < p < 1 . On the other hand, when
E = 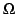 (or
E =
(or
E = 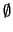 ) there is no uncertainty on the outcome of the corresponding bet:
the only (certain!) value of the gain is
G(
) there is no uncertainty on the outcome of the corresponding bet:
the only (certain!) value of the gain is
G(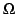 ) = - p + 1 or
G(
) = - p + 1 or
G( 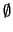 ) = - p respectively, and so coherence requires that the gain is equal to
zero, which gives p = 1 for
E =
) = - p respectively, and so coherence requires that the gain is equal to
zero, which gives p = 1 for
E = 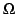 and p = 0 for
E =
and p = 0 for
E = 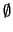 .
In conclusion, if the subjective probability of E (our degree of belief in
E) is defined as an amount p = P(E) which makes coherent a bet on E,
then
0
.
In conclusion, if the subjective probability of E (our degree of belief in
E) is defined as an amount p = P(E) which makes coherent a bet on E,
then
0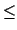 P(E)
P(E)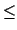 1.
1.
And what about the case of n simultaneous bets on the events
E1, E2,..., En of a partition of 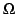 ? Let
P(Ek), k = 1, 2,..., n, be the
amount paid for a coherent bet on Ek. Clearly, these n bets can be
regarded as a single bet on
? Let
P(Ek), k = 1, 2,..., n, be the
amount paid for a coherent bet on Ek. Clearly, these n bets can be
regarded as a single bet on 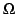 with amount
P(E1) + P(E2) + ... + P(En),
and so coherence requires
P(E1) + P(E2) + ... + P(En) = 1.
with amount
P(E1) + P(E2) + ... + P(En),
and so coherence requires
P(E1) + P(E2) + ... + P(En) = 1.
So the usual ``axioms" of probability are easily obtained in a very simple
way, through coherence. It is important to stress the fact that, even if the
intuitive semantic interpretation of coherence is expressed in terms of
(hypothetical!) bets, this circumstance must not hide the fact that its role
(that of ruling probability evaluations concerning ``many" events) is
essentially syntactic.
The ``combinatorial" and ``frequentist" methods of evaluation of
probabilities can be easily embedded (the latter through exchangeability)
into the general concept of subjective probability. Let me point out that
this approach puts in the right perspective all
the subjective aspects hidden in the so-called ``objectivistic theories".
I cannot go here into further details, so I just mention two of my articles
(Subjective probability and Bayesian statistics in engineering
mathematics education, Int. J. Math. Educ. Sci. Technol., 1987, vol.18, n.5,
685-688; A merged approach to stochastics in Engineering Curricula,
European J. Eng. Educ., 1990, vol.15, n.3, 243-250), and - for
conditional probability - my short note (Probability assessment and
Bayesian inference) in the ISBA Newsletter, Issue n.3, September 1994.
I wrote also an elementary text (in Italian, but the title needs not a
translation!): Probabilità soggettiva: significato, valutazione,
applicazioni, Masson (first edition 1989, fourth edition 1997).
ISBA Newsletter, June 1999 APPLICATIONS
RATING COMPETITORS IN ONLINE GAMES
by Mark E. Glickman
mg@math.bu.edu
A new Bayesian rating system gradually becomes accepted on
popular online game servers.
It's a cold, wet Saturday afternoon, so you're stuck inside.
What do you do? Some data analysis? Prove a theorem?
No - now is the time to log onto one of many internet game
servers and spend the rest of the day competing against others
like you in games such as chess, bridge, fantasy baseball,
or a role-playing adventure game.
The opportunities to play with other humans through internet game
servers has increased dramatically over the past several years.
Some of the major internet companies like Yahoo,
Excite, and Netscape have created their own game areas on
which, upon registration, anyone can obtain free access.
Typical game servers have anywhere from hundreds to tens of
thousands of players online simultaneously.
To make competing more enjoyable and interesting,
many internet gaming organizations have set up rating
systems on their servers.
Ratings allow players to assess their skill level,
and let them compare their own playing strengths against others.
Arguably, the most commonly implemented rating system on
internet game servers is due to Arpad Elo, the creator of
a popular system for rating tournament chess players.
The system is described in detail in his 1978 monograph
(The Rating of Chess Players, Past and Present, Arco, 1978).
The basic idea of this system is that every player obtains
a rating through competition, and this rating changes over
time based on the player's results.
In typical implementations of Elo's system, ratings range
between 0 and 3000, with higher ratings connoting stronger skill.
When two players of equal rating compete, the winner gains
16 rating points and the loser loses 16.
Defeating a player with a higher rating results in a rating
gain of more than 16 points, and defeating an opponent with
a lower rating results in a gain of fewer than 16 points.
Similarly, players defeated by stronger players will lose
fewer than 16 points, and will lose more than 16 points if
defeated by a weaker player.
Essentially Elo's system is a particular non-linear filter on ratings
as a function of game outcomes.
The formulas to calculate ratings are so simple that they can
easily be carried out using pencil and paper.
A rating system for internet game competitors can be viewed
as a method for estimating parameters of a time-series model.
Every player possesses an unknown strength parameter at a
given point in time, but the strength parameters change
stochastically over time.
The goal of the rating system is to infer these parameters.
The Elo system produces point estimates of the strength
parameters after every competition by essentially
performing a calculation that approximates a weighted
average between the pre-game rating and a game ``performance'' rating.
Thus, to first approximation, the Elo system has a Bayesian
flavor: the pre-game rating is treated analogously to a prior, and
the information in a game is treated similarly to the likelihood.
Despite the simplicity and popularity of Elo's system,
there are several obvious problems.
One of the main problems is that the system does not
recognize the uncertainty in players' ratings.
To understand why this is a problem,
suppose a player rated 1500 is about to compete
against an opponent.
If the player's 1500 rating is based on very few game
results, so that the 1500 rating is an imprecise estimate of
the player's ability, then it would seem reasonable that the
game outcome should have a substantial impact on the
player's post-game rating.
This would be equivalent to assuming a vague
prior on the player's strength so that the
likelihood mostly determines the posterior.
On the other hand, the player's rating of 1500 may
be a precise measure (because, for example, the player
competes often), in which case the outcome of a single game
should not have an appreciable effect on the estimate of the
player's strength.
Elo's system does not make any distinction between these two
situations.
ISBA Newsletter, June 1999 APPLICATIONS
A forthcoming article in Applied Statistics
(Glickman, Mark E. (1999) ``Parameter estimation in large dynamic paired
comparison experiments'')
develops a rating system for competitors that
adheres more carefully to a Bayesian framework.
Instead of merely providing point estimates of players'
skill parameters, the system produces an approximate Gaussian
posterior distribution.
Thus every player has both a rating (the posterior mean)
and an estimate of its uncertainty (the posterior variance).
One of the main advantages of this new system is that
not only is the posterior uncertainty in a player's strength
quantified, but the uncertainty measure is used in the calculations
to update players' strength estimates.
Prior to a competition, players with large prior variances
will potentially undergo dramatic changes from prior to
posterior means.
Another feature of the system is that players' strength
parameter variances increase over time while not competing.
This reflects the notion that there is greater uncertainty
in a player's ability as time passes if no evidence of
ability is presented.
The development of the rating system in the Applied
Statistics article demonstrates how a simple rating system
can be derived through various approximations
as a Bayesian analysis of a state-space model.
The article demonstrates how the Elo system can be viewed as
a special case of the Bayesian system under the assumption
that players' strengths are known with certainty, which, of
course, is never the case.
The rating system is applied to the analysis of a dataset
consisting of all known games between the best chess players
of all time, and to the analysis of recent tennis matches among
1100 professional players competing in the ATP Tour.
This new system (now being called the ``Glicko'' system),
is currently used by several internet game servers.
The ``Free Internet Chess Server,''
for example,
has been using this system for several years.
More recently, this Bayesian system has been adopted by
commercial organizations such as Case's ladder, a multi-player
gaming league with over a million members who can compete in
various internet games.
It has also been adopted in role-playing adventure games
such as Chron X.
For readers who are interested in the system's implementation
without the theoretical underpinnings, they can be found
at the web site http://math.bu.edu/people
/mg/ratings.html.
ISBA Newsletter, June 1999 BIBLIOGRAPHY
EPIDEMIOLOGY
by Siva Sivaganesan
siva@math.uc.edu
We present an annotated bibliography of Bayesian applications in Epidemiology.
To date Bayesian ideas have had limited impact on the practice of
epidemiological research (as distinct from the development of
biostatistical methodology where Bayesian methods seem to be more widely used),
but this may be changing.
For instance, the following paper by Sander
Greenland presents a very interesting philosophical discussion promoting
the role of subjective probability arguments in epidemiological analysis:
[0.7mm]  S. GREENLAND (1998).
Probability Logic and Probability Induction.
Epidemiology 9(3), pp322-32.
S. GREENLAND (1998).
Probability Logic and Probability Induction.
Epidemiology 9(3), pp322-32.
Contact: Sander Greenland, UCLA School of Public Health, USA.
In this paper the author defines the notion(s) of probability, and argues that
probability logic recognizes prior distribution as an integral part of
statistical analysis, rather than the current misleading practice, in Epidemiology, of pretending that statistics applied to observational data are objective. After presenting arguments in favor of the subjective prior approach, as opposed to the objective or non-informative prior approach,
the author suggests that a hierarchical Bayes or empirical Bayes approaches may fall in between the two, and that these are well suited to many epidemiological studies.
The significance of the above paper was highlighted by a short editorial by
another prominent epidemiologist, Malcolm Maclure, in the same issue of the
journal (Epidemiology 1998;9(3):p233), entitled "How to Change Your
Mind". This piece describes how the author has been persuaded to
Greenland's point of view, and highlights the fact that epidemiology has
been dominated by the traditional fear of "subjectivity", presumably
inculcated by long exposure to frequentist statistical dogmas.
Another recent paper presents a simple discussion of the pragmatic
application of Bayesian "uniform-prior" or non-informative prior approach:
[0.7mm]  P. R. BURTON, L. C. GURRIN AND M. J. CAMPBELL (1998).
Clinical significance not statistical significance: a simple
Bayesian alternative to p values .
Journal of Epidemiology & Community Health 52(5); pp318-23.
P. R. BURTON, L. C. GURRIN AND M. J. CAMPBELL (1998).
Clinical significance not statistical significance: a simple
Bayesian alternative to p values .
Journal of Epidemiology & Community Health 52(5); pp318-23.
Contact: P. R. Burton, TVW Telethon Institute for Child Health Research, West Perth, Australia.
In the above paper the authors
state that the frequentist confidence intervals have a
Bayesian uniform prior interpretation, and that inference constructed using the corresponding posterior distribution is
more informative and more easily understood. They illustrate this by using existing frequentist results from a public health study,
and using them to make posterior probability statements, with respect to uniform prior,
that are useful in interpreting these results and help in public policy decision making. They predict that with the arrival of general purpose Bayesian software, such as BUGS, it is probable that Bayesian analysis will become common place.
Also, in the book:
 KENNETH J. ROTHMAN AND SANDER GREENLAND (1998).
Modern Epidemiology, 2nd. Ed
KENNETH J. ROTHMAN AND SANDER GREENLAND (1998).
Modern Epidemiology, 2nd. Ed
parts of various chapters are devoted to the foundation and application of Bayesian methods as applicable to Epidemiology. The authors specifically argue that
in non-experimental studies, the so-called objective frequentist methods
(such as the significance tests and confidence intervals) lack the objective
repeated-sampling properties, and that a rational (if subjective)
assessment may be the only thing of interest that one can get out of a statistical analysis of observational epidemiological data.
Another article promoting the use of Bayesian methods is:
 R. J. LILFORD AND D. BRAUNHOLTZ (1996).
The statistical basis of public policy: a paradigm shift is
overdue.
British Medical Journal , 313(7057) : pp603-7.
R. J. LILFORD AND D. BRAUNHOLTZ (1996).
The statistical basis of public policy: a paradigm shift is
overdue.
British Medical Journal , 313(7057) : pp603-7.
Contact: R. J. Lilford, University of Birmingham, UK.
Here, it is argued that the conventional statistical tests and estimates are an improper basis for public policy as they dichotomize results according to whether
or not they are
ISBA Newsletter, June 1999 BIBLIOGRAPHY
significant, thereby tending to produce an on/off response by decision makers. They state that health issues are much more complex and that only the Bayesian approach can provide the probabilistic basis for appropriate action or inaction in public policy matters relating to environmental health.
Other articles using Bayesian and related methodology include:
 P. JORDAN, D. BRUBACHER, S. TSUGANE, Y. TSUBONO, K. F. GEY AND U. MOSER (1997).
Modeling of mortality data from a multi-center study in Japan by means of
Poisson regression with error in variables .
Int. J. Epidemiology 26(3), pp501-7.
P. JORDAN, D. BRUBACHER, S. TSUGANE, Y. TSUBONO, K. F. GEY AND U. MOSER (1997).
Modeling of mortality data from a multi-center study in Japan by means of
Poisson regression with error in variables .
Int. J. Epidemiology 26(3), pp501-7.
Contact: Paul Jordon, Hoffmann-La Roche Ltd., Basel, Switzerland.
Here, relative risk of stomach cancer associated with plasma lycopene level in age-specific populations was modeled using a Poisson regression model with over dispersion and errors in variables. The authors comment that the Bayesian approach allow the estimation of the relative risk in their study with small sample sizes and low number of cases.
 J. S. WITTE, S. GREENLAND, R. W. HAILE AND C. L. BIRD (1994).
Hierarchical regression analysis applied to a study of multiple dietary
exposures and breast cancer.
Epidemiology 5(6), pp612-21.
J. S. WITTE, S. GREENLAND, R. W. HAILE AND C. L. BIRD (1994).
Hierarchical regression analysis applied to a study of multiple dietary
exposures and breast cancer.
Epidemiology 5(6), pp612-21.
Contact: John S. Witte, Case Western Reserve University, USA.
In the above article a hierarchical regression approach is used, where a regression model using a new set of underlying covariates is used in the second stage, to
estimate the effects of certain dietary exposures to breast cancer. Here, in what the authors call a semi-Bayes approach, the second stage standard deviation is specified through subjective elicitation and the models in the first stage is fitted first, and the results are used in fitting the second stage model. This approach gives more stable and plausible estimates than the one-stage
maximum likelihood logistic regression.
 L. WATIER, S. RICHARDSON, D. HEMON (1997).
Accounting for pregnancy dependence in epidemiologic studies of reproductive
outcomes.
Epidemiology 8(6), pp629-36.
L. WATIER, S. RICHARDSON, D. HEMON (1997).
Accounting for pregnancy dependence in epidemiologic studies of reproductive
outcomes.
Epidemiology 8(6), pp629-36.
Contact: L. Walter, Institut National de la Sante et de la Recherche Medicale, France.
Contribution of hierarchical mixed models to the analysis of epidemiologic studies of environmental exposure and reproductive outcomes
is evaluated. A logistic-normal mixed model is fitted using Bayesian and maximum likelihood approaches to data from four studies investigating the relation between the frequency of spontaneous
abortions and paternal or maternal environmental exposures. The fitted models allow for between-woman
variation of the propensity for spontaneous abortion, by including a random
intercept in the logistic model to adjust for within-woman correlations on
pregnancy outcomes.
We are helpful to John B. Carlin of University
of Melbourne, Australia for his help on some of the references.
ISBA Newsletter, June 1999 STUDENT'S CORNER
RECENT RESEARCH
by Sudipto Banerjee
sudipto@stat.uconn.edu
We present some abstracts by Ph.D. students.
Ilaria Di Matteo is a Ph.D candidate
under the supervision of Dr. R. Kass in Carnegie Mellon University, Pittsburgh.
Ilaria has worked on Bayesian Curve Fitting using Spline functions. We also
present abstracts of two papers from CMU. Both of them have been sent by
J. R. Lockwood, a graduate student at CMU. The first paper deals with modelling
the distribution of arsenic in water treatment systems under a Bayesian
Hierarchical set-up. He is co-authored by Professor M. Schervish of the
Department of Statistics at CMU, Patrick Gurian, a graduate student in
the Department of Engineering and Public Policy, and Professor Mitchell Small
of the Department of Engineering and Public Policy and Civil Engineering. His
second contribution is a paper in Statistical genetics co-authored by
Professor Kathryn Roeder of the Department of Statistics in CMU and Professor
Bernie Devlin of the Department of Psychiatry in the University of Pittsburgh.
We present an abstract from the dissertation by Herbert Lee of the
Department of Statistics at CMU. He completed his Ph.D. in December 1998. He
has developed a methodology to perform Bayesian non-parametric regression using
neural networks. We finally present the abstracts of three recent Italian
Ph.D. dissertations.
Papers at
Carnegie Mellon University
Ilaria DeMatteo
dimatteo@stat.cmu.edu
Bayesian Curve Fitting using Splines
Advisor: Robert Kass
Regression splines represent a very flexible tool to estimate
curves, but they heavily rely on the choice of the number of knots ad
their location. Several methods have been suggested to search for the
optimal knot location. We propose a Bayesian method in which the
number of knots and their locations are considered parameters, and
their posterior distributions are computed through reversible-jump
Markov Chain Monte Carlo. The advantage of our model compared to that
of Denison Mallick and Smith (1998 JRSS B), is that reduces
significantly the Mean Square Error, MSE, of the fitted curves. Also,
from a small simulation
study, our model seems to produce curves having smaller MSE than the
Spatially Adaptive Regression Spline developed by Zhou and Shen (1999
Annals of Statistics). A generalization to hierarchical models
has been implemented and is currently being studied. We are also
developing spline-based curve-fitting methods for non-Normal data.
J. R. Lockwood, Mark J. Schervish, Patrick Gurian and Mitchell Small
jlock@stat.cmu.edu mark@stat.cmu.edu gurian+@andrew.cmu.edu ms35+@andrew.cmu.edu
The 1996 amendments to the US Safe Drinking Water Act mandate revision
of current maximum contaminant levels (MCLs) for various harmful
substances in public drinking water supplies. The determination of a
revised MCL for any contaminant must reflect a judicious compromise
between the potential benefits of lowered exposure and the feasibility
of obtaining such levels. This regulatory impact assessment requires
detailed information about both occurrence of the contaminant and the
costs and efficiencies of the available treatment technologies. Our
work focuses on the first step of this process, using a collection of
data sources to model arsenic occurrence in treatment facility source
waters as a function of system characteristics such as source water
type, location and size. We fit Bayesian hierarchical models to
account for the spatial aspects of arsenic occurrence as well as to
characterize uncertainty in our estimates. After model selection
based on cross-validation predictive densities, we use a national
census of treatment systems and their associated covariates to predict
the national distribution of raw water arsenic concentrations. We
then examine the relationship between proposed MCL and the number of
systems requiring treatment augmentation and we identify classes of
systems which are most likely to be problematic.
ISBA Newsletter, June 1999 STUDENT'S CORNER
The posterior
distribution of the model parameters, obtained via Markov Chain Monte
Carlo, allows us to quantify the uncertainty in our predictions.
J. R. Lockwood, Kathryn Roeder and Bernie Devlin
jlock@stat.cmu.edu roeder@stat.cmu.edu devlinbj@msx.upmc.edu
Many applications in statistical genetics, such as linkage analysis,
require accurate estimates of allele frequencies for populations
which may have different evolutionary histories. Given allele
counts for a collection of loci and populations, we propose a
Bayesian hierarchical model which extends existing empirical
Bayesian approaches by allowing for explicit inclusion of prior
information about both allele frequencies and inter-population
divergence. We describe a methodology for obtaining informative
prior distributions for model parameters based on previous research.
Using simulated data, we present an application of the model and
highlight the features of the data which are incorporated with our
structure. We also provide references and partial documentation for
our publicly-available code for fitting the model.
Herbert Lee
herbie@stat.cmu.edu
Model Selection and Model Averaging for Neural Networks
Advisor: Larry Wasserman
Neural networks are a useful statistical tool for nonparametric
regression. In this thesis, I develop a methodology for doing
nonparametric regression within the Bayesian framework. I address the
problem of model selection and model averaging, including estimation
of normalizing constants and searching of the model space in terms of
both the optimal number of hidden nodes in the network as well as the
best subset of explanatory variables. I demonstrate how to use a
noninformative prior for a neural network, which is useful because of
the difficulty in interpreting the parameters. I also prove the
asymptotic consistency of the posterior for neural networks.
1999 Ph.D's
at Università di Trento,
Italy
Ilenia Epifani
ilenia@iami.mi.cnr.it
Some results about Random Bernstein Polynomials and their
applications to Bayesian nonparametric inference
Advisor: Eugenio Regazzini
In our dissertation we deal with the Bernstein measure recently
suggested by Sonia Petrone as prior distribution to determine a
Bayesian nonparametric density estimation for observations in the
closed interval [0, 1].
The basic idea of Bernstein measure is simple: every probability
distribution function (df) F on [0, 1] can be approximated with the
Bernstein polynomial
B(
K,
F,
x) =
1(1,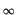 )
)(
x) +
1[0, 1](
x)
.
when K and F are random with law Q, the distribution of random
Bernstein polynomial B (which is a measure probability on the space
of all df on [0, 1]), is called Bernstein prior of parameter
Q. If K is an integer valued random variable with law h, F is
a Ferguson-Dirichlet random distribution function (rdf ) with law d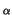 and Qis equal to the product measure, then the law of B(K, F) is called
Bernstein-Dirichlet prior of parameters
h, d
and Qis equal to the product measure, then the law of B(K, F) is called
Bernstein-Dirichlet prior of parameters
h, d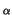 . The Bernstein-Dirichlet measure
shares the ``large'' support of the Ferguson-Dirichlet one and selects continuous
distributions with probability 1. Our attention is focused on the
characterization of the finite-dimensional laws of the Bernstein-Dirichlet measure
through the explicit expressions of mixed moments, derived from the
moment-generating function, which is established for the first time in
our work.
. The Bernstein-Dirichlet measure
shares the ``large'' support of the Ferguson-Dirichlet one and selects continuous
distributions with probability 1. Our attention is focused on the
characterization of the finite-dimensional laws of the Bernstein-Dirichlet measure
through the explicit expressions of mixed moments, derived from the
moment-generating function, which is established for the first time in
our work.
Furthermore, we give a recurrence formula for the mixed-moments which
can be used for the numerics. Finally, we determine the posterior
distribution of random Bernstein-Dirichlet polynomial B: if
X1,..., Xn,... are
conditionally i.i.d. given B(K, F), the posterior distribution of
B(K, F) | X1,..., Xn is a Bernstein measure with parameters
hn(k),
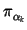 where hn denote the conditional
distribution of
K | X1,..., Xn and
where hn denote the conditional
distribution of
K | X1,..., Xn and
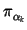 is a
suitable mixture of Ferguson-Dirichlet measures
is a
suitable mixture of Ferguson-Dirichlet measures
ISBA Newsletter, June 1999 STUDENT'S CORNER
which coincides with the posterior
distribution of
B(K, F) | K, X1,..., Xn. Then we investigate
the distribution of some functionals of B(K, F): for the mean
functional we give the df and moment-generating function, whereas for
the variance functional we obtain only the moments of any order. The
first part of the dissertation ends with a suggested prior
distribution of Bernstein-Dirichlet kind for observations taking values in [0, 1]mwhich extends the one given by Petrone for the [0, 1] case. Besides
the finite-dimensional laws and posterior distribution, we give the
laws of some remarkable functionals as the means vector and variances
and covariances matrix. Moreover a Bayesian nonparametric estimation
of a multivariate density is given.
In the second part of the dissertation, the results about the random
Bernstein-Dirichlet polinomials are utilized to investigate some
properties of the Ferguson-Dirichlet rdf . We give the moments of the mean of a Ferguson-Dirichlet rdf with parameter 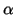 ,
,
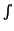 g(x)dF
g(x)dF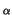 , for every measure
, for every measure
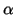 . In particular, if the support of
. In particular, if the support of 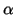 is limited, we
use as main tool of our investigation the weak convergence of a
sequence of random Berstein-Dirichlet polynomials to the Ferguson-Dirichlet rdf . On
the other hand, when the support of
is limited, we
use as main tool of our investigation the weak convergence of a
sequence of random Berstein-Dirichlet polynomials to the Ferguson-Dirichlet rdf . On
the other hand, when the support of 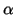 is unlimited, we
construct a suitable sequence of uniformly integrable random variables
converging in probability to the mean functional of F
is unlimited, we
construct a suitable sequence of uniformly integrable random variables
converging in probability to the mean functional of F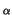 , such
that the moments of those random variable can be easily computed.
Hence, we have carried out a similar investigation for the moments of
the variance of a Ferguson-Dirichlet rdf on
R and for the mixed moments
of the means vector and the covariance matrix of a Ferguson-Dirichlet rdf on
Rm. The tecniques in the proof of the previous results
can be applied to the cases in which the statistical analysis leads to
consider simultaneously many ``typical values'' of the unknown df Fof the kind
, such
that the moments of those random variable can be easily computed.
Hence, we have carried out a similar investigation for the moments of
the variance of a Ferguson-Dirichlet rdf on
R and for the mixed moments
of the means vector and the covariance matrix of a Ferguson-Dirichlet rdf on
Rm. The tecniques in the proof of the previous results
can be applied to the cases in which the statistical analysis leads to
consider simultaneously many ``typical values'' of the unknown df Fof the kind
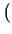
 Rg1(x)dF
Rg1(x)dF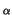 ,...,
,..., Rgm(x)dF
Rgm(x)dF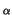
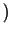 .
.
Antonio Lijoi
antonio@iami.mi.cnr.it
Approximating priors by finite mixtures of conjugate
distributions for an exponential family
Advisor: Eugenio Regazzini
If the statistical model belongs to an exponential family, it is well-known
in Bayesian statistics that any prior can
be approximated, in the Prokhorov metric, by a suitable finite mixture of
conjugate priors. However, no rule for concretely constructing such a
mixture is provided. Taking this remark as a starting point, in the
dissertation an estimate of the error of approximation is initially given
for some special cases. Three examples are considered:
Poisson, Bernoulli and Normal model. Correspondingly,
once a prior p.m. and a positive 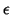 are fixed, a set of values for the hyperparameters of the conjugate
distributions and a minimum number k of summands in the mixture
are found such that
the error of approximation does not exceed
are fixed, a set of values for the hyperparameters of the conjugate
distributions and a minimum number k of summands in the mixture
are found such that
the error of approximation does not exceed 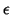 .
.
An analogous estimate is provided with reference to the posterior
distribution. In other words,
the above-mentioned models are taken in consideration and values of the
hyperparameters and of the number of elements in mixture are given such
that the error of approximation for the prior as well as for the posterior
does not exceed 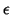 .
Proofs of these results rely upon the fact that mixtures of point
masses are dense, in the topology of weak convergence,
and upon the application
of a Large Deviations estimate to the conjugate distributions.
Bounds for the hyperparameters and for the value to be
assigned to k suggest that the posterior obtained
form the finite mixture converges weakly to the posterior corresponding
to the approximated prior, but this convergence is not uniform with
respect to the observed sample.
.
Proofs of these results rely upon the fact that mixtures of point
masses are dense, in the topology of weak convergence,
and upon the application
of a Large Deviations estimate to the conjugate distributions.
Bounds for the hyperparameters and for the value to be
assigned to k suggest that the posterior obtained
form the finite mixture converges weakly to the posterior corresponding
to the approximated prior, but this convergence is not uniform with
respect to the observed sample.
The final part of the dissertation is devoted to the formulation of a
generalization of previous results to any natural
exponential family. Unfortunately, in the general case it is not possible
to resort to any kind of Large
Deviations estimate. Hence, the method applied in special cases cannot
be used and explicit bounds for the hyperparameters and for k are not
available. However, by means of the Laplace's method,
rates of convergence of the approximating mixtures to the prior
and to the posterior distribution are determined.
ISBA Newsletter, June 1999 STUDENT'S CORNER
Claudia Tarantola
claudia@verdea.stats.aueb.gr
Bayesian Model determination for Discrete Graphical Models
Advisor: Guido Consonni
A graphical model is a family of probability distributions incorporating
the conditional independence assumptions represented by a graph. It is
constructed by specifying local dependencies of each node of the graph
in terms of its immediate neighbours. It is then possible to work locally,
obtaining better results in terms of
statistical inference and computational efficiency.
In this thesis we fix our attention on the case in which all considered
variables are discrete, and the graph is undirect. Furthermore, we consider
a particular subclass of graphical models, the so called decomposable models.
These models present special features that make the learning process easier.
Our objective is to make inference both on the graphical structure,
quantitative learning, and on the parameters characterising the
considered distributions, qualitative learning. In order to do this,
for each given graph, we assign an Hyper Dirichlet distribution (Dawid and
Lauritzen 1993) on the matrix of cell probabilities; such a prior
distribution is obtained by marginalisation from the prior conditional on
the complete graph.
This not only ensure compatibility across models, but also leads to a
prior distribution automatically satisfying the hyperconsistency criterion.
Finally, we assign a uniform prior on the class of decomposable graphs.
One problem related to the analysis of graphical models
is that the number of structure under comparison increases more
than exponentially with the number of nodes; for high-dimensional
contingency tables the set of plausible models is large,
and a full comparison of all the posterior probabilities associated to the
competing models becomes infeasible. Hence the necessity to construct
computational algorithms able to explore
efficiently the space of all possible models.
Various solutions to this problem have been proposed,
the one we suggest is based on the
application of Markov chain Monte Carlo techniques (MCMC).
Related works in the area are the one by Madigan and York (1995),
that introduce an MCMC sampler, called Markov chain Monte
Carlo composition (MC3), for the analysis of decomposable models
and the one by Dellaportas and Foster (1999) who develop a MCMC
sampler for model choice in the general class of loglinear models.
In this thesis we present two different samplers which
are fully based on local computations and are therefore efficient.
The first sampler is a
revised version of the MC3 algorithm by Madigan and York (1995).
It differs from the original version mainly because it
incorporates a local condition
for checking decomposability, see Giudici and Green (1999).
Furthermore, we propose an extension which allows
for a hierarchical prior on the cell counts.
The second sampler is based on the Reversible Jump by Green (1995).
Our methodology parallels that presented in Giudici and Green (1999)
for the analysis of decomposable gaussian models.
As in the gaussian case, at each step of the algorithm we update not only
the graphical structure (as in MC3), but also the associated parameter
vector. Essentially, in the gaussian case, pairwise conditional
independence is dictated
by the absence of a single parameter, whereas in the discrete case this
generally corresponds to non linear constraints on the cell probabilities.
Furthermore, in the continuous case the parameter space is polynomial
in the number of variables whereas in the
discrete case it is exponential. This leads to substantial differences in the
data structure.
The performance of the two samplers has been tested with reference to
the Women and Mathematics data set, well known in the graphical model
literature.
ISBA Newsletter, June 1999 GREECE
BAYESIANS
IN GREECE
by Petros Dellaportas
petros@aueb.gr
``Well, Petros, you are not the first Greek I know who decided to
continue his career in Greece. But you should do a lot of travelling if
you want to keep up with good research''. Those were the words of
Adrian Smith back in 1990 when I told him that my next career step would
be the Greek national service and a consequent permanent settlement in
Greece. He had visited Greece back in 1987 and he knew that there are
not that many Greek academics interested in Bayesian Statistics.
The other Greek Bayesian Statistician Adrian meant was George Kokolakis.
George got his Ph.D. from University College London in 1978 under the
supervision of Dennis Lindley. Then George returned to Greece and he
has been working at the National Technical University of Athens since
then. He has been the first Bayesian in Greek academia, something who
himself sometimes regrets: ``It is the first time in my life that I
discuss research in my native language and it is both nice and strange''
he told me when we first met in 1991. George was the first to introduce
Bayesian ideas to Greek University students and he was, for many years,
the sole Greek Universities representative in the Bayesian conferences.
My first position was at the recently established (1989) Department of
Statistics (www.stat-athens.aueb.gr/)
of the Athens University of Economics and Business (AUEB). To my
surprise, the department undergraduate syllabus contained a course in
``Bayesian Statistics''. I have been teaching the course since 1993,
-the colleague who was teaching the course was extremely pleased to pass
it to me: he confessed to me that he did not agree with a single word of
what he was teaching.
A course in Bayesian statistics was a great chance to promote Bayesian
thinking and now the department has some active Bayesian life. First,
some postgraduate courses
(non-linear models, generalised linear models) have obtained some
Bayesian flavor and our MSc graduates can perform quite demanding
analyses of data using BUGS. Second, Yiannis Ntzoufras, the first Greek
Bayesian Ph.D. student, submitted his thesis on ``Aspects of Bayesian
Model and Variable Selection Using MCMC'' last month. There are 3 other
Ph.D. students, Stefanos Giakoumatos, Mihalis Linardakis and Yiannis
Vrontos, currently working on Bayesian problems. They are all expected
to finish by the end of next year. And finally, there is a plethora of
MSc dissertations written by students who adopt a Bayesian perspective
in their analysis. As a result of all this, there are now some
colleagues (Dimitris Karlis, Harry Pavlopoulos, Evdokia Xekalaki) who
have adopted a Bayesian viewpoint in some of their research
activities. Last but not least, Dimitris Politis who is currently
based at University of California, San Diego,
visits our department very often and has been
collaborating with our research group adopting Bayesian approaches.
Although in AUEB the Bayesian group seems to be vivid, there is little
happening outside its doors. An interesting exception is Maria Kateri
and Takis Papaioannou from the department of mathematics of University
of Ioannina who have been working on symmetry and asymetry models for
contingency tables from a classical perspective. After publishing a
series of papers using classical methodologies, they have recently
started exploring these problems adopting a Bayesian viewpoint.
Another Bayesian who has recently returned to Athens is Thanasis Katsis,
who received his PhD on Baysian Optimal Experiments for Discrete
Distributions at George Washington University
under the supervision of Blaza Toman. He is currently doing his
national service.
However, we hope that our group will grow. Take for example the list of
Bayesians below (you can find this list at
www.stat-athens.aueb.gr/~jbn/
grstats_Bayes.htm). They are not in
Greece, but they are Greek. I hope that some of them, if not all, will
be in Greek universities some day. Then Adrian might change his
wordings to the young Greeks who decide to come back to something like
``the research group in Greece is really good, and the sun is shining: I
cannot see why you should stay in UK!''
ISBA Newsletter, June 1999 GREECE
228 Greek Bayesians outside Greece
 Aslanidou Vlachos Helen, Msc graduate (Univ. of
Connecticut), Epidemiology Data Center, Univ.of Pittsburgh,
ruddles.stat.uconn.edu/
Aslanidou Vlachos Helen, Msc graduate (Univ. of
Connecticut), Epidemiology Data Center, Univ.of Pittsburgh,
ruddles.stat.uconn.edu/~helen/.
 Fouskakis Dimitris, Ph.D. Student, School of
Mathematical Sciences, University of Bath, UK,
www.bath.ac.uk/
Fouskakis Dimitris, Ph.D. Student, School of
Mathematical Sciences, University of Bath, UK,
www.bath.ac.uk/~mapdf/.
 Frangakis Constantin, Graduate Student, Dep.
of Statistics, Harvard University,
frangaki@stat.harvard.edu.
Frangakis Constantin, Graduate Student, Dep.
of Statistics, Harvard University,
frangaki@stat.harvard.edu.
 Gatsonis Costantine, Associate Professor, Center for
Statistical Sciences, Brown University,
alexander.stat.brown.edu/
hpages/gatsonis.html.
Gatsonis Costantine, Associate Professor, Center for
Statistical Sciences, Brown University,
alexander.stat.brown.edu/
hpages/gatsonis.html.
 Kornak John, PhD. Student, School of Mathematical
Sciences, University of Nottingham,
www.maths.nott.ac.uk/
people/jk.html.
Kornak John, PhD. Student, School of Mathematical
Sciences, University of Nottingham,
www.maths.nott.ac.uk/
people/jk.html.
 Melas Dina, PhD Student, Statistics Department,
Trinity College, Dublin (Ireland), melasd@tcd.ie.
Melas Dina, PhD Student, Statistics Department,
Trinity College, Dublin (Ireland), melasd@tcd.ie.
 Papandonatos George, Center for Statistical Sciences,
Brown University, gdp@stat.brown.edu.
Papandonatos George, Center for Statistical Sciences,
Brown University, gdp@stat.brown.edu.
 Papathomas Michalis, University of Nottingham, PhD
Student, mpa@maths.nott.ac.uk.
Papathomas Michalis, University of Nottingham, PhD
Student, mpa@maths.nott.ac.uk.
 Skouras Kostas, Lecturer, Dept. of Statistical Science,
University College London,
www.ucl.ac.uk/
Skouras Kostas, Lecturer, Dept. of Statistical Science,
University College London,
www.ucl.ac.uk/
~ucakks1/home.html.
 Spiropoulos Takis, University of Hertfordshire,
t.spiropoulos@herts.ac.uk.
Spiropoulos Takis, University of Hertfordshire,
t.spiropoulos@herts.ac.uk.
 Streftaris Giorgos, PhD Student, gst@maths.ed.ac.uk.
Streftaris Giorgos, PhD Student, gst@maths.ed.ac.uk.
 Vlachos Pantelis, Visiting Research Scientist, Department
of Statistics, Carnegie Mellon University,
www.stat.cmu.edu/
Vlachos Pantelis, Visiting Research Scientist, Department
of Statistics, Carnegie Mellon University,
www.stat.cmu.edu/~vlachos/.
 Vounatsou Penelope, Post-doc, Dept. of Public Health and
Epidemiology, University of Basel
www.wb.unibas.ch/sti/
personel/VOUNATSP.htm.
Vounatsou Penelope, Post-doc, Dept. of Public Health and
Epidemiology, University of Basel
www.wb.unibas.ch/sti/
personel/VOUNATSP.htm.
 Yiannoutsos Constantin, Research Associate, Dep.
of Biostatistics, Harvard University, costas@hsph.harvard.edu.
ISBA Newsletter, June 1999 NEWS FROM THE WORLD
Yiannoutsos Constantin, Research Associate, Dep.
of Biostatistics, Harvard University, costas@hsph.harvard.edu.
ISBA Newsletter, June 1999 NEWS FROM THE WORLD
NEWS FROM THE WORLD
by Antonio Pievatolo
marco@iami.mi.cnr.it
228 Events
Second Mexico Workshop on Bayesian Statistics. August
25-27, 1999. Mexico City.
The workshop is sponsored by the Mexican Statistical Association. The
programme's central activity will be the short course ``Bayesian
Biostatistics'', by Andrew Gelman (Columbia University, USA).
Contributed papers will be presented in a plenary poster
session; a title and an abstract should be sent by the end of July.
INFO: tameb@sigma.iimas. unam.mx
ICES Annual Science Conference. September 29 to
October 2, 1999. Folkets Hus, Stockholm, Sweden.
One of the theme sessions of the 1999 ICES (International Council for the
Exploration of the Sea) Annual Science Conference is on
``Bayesian Approach to Fisheries Analysis''. The Bayesian methods
can provide a powerful basis for quantifying
the uncertainty in stock assessments and, when coupled with decision
analysis, provide a natural means of communicating this uncertainty to
fishery managers, e.g., the short and long-term consequences of candidate
management actions.
Contributions illustrating the state-of-the-art application of
methods for stock assessment and managment and summarising
the pros and cons of the Bayesian approach will be presented.
Registration must be made by August 31.
INFO: http://www.ices.dk or contact
Ms M. Azevedo (mazevedo@ipimar.pt)
Foundational Issues and Statistical Practice. October 14-16, 1999. Bibbiena (Arezzo), Italy.
This workshop is co-sponsored by the Italian Statistical Society (SIS),
the Italian Institute of Official Statistics (ISTAT)
and the Bank of Italy.
The scientific programme features 8 invited
lectures. The focus of the workshop is on how
the conclusions of an analysis can depend on which inferential
paradigm has been adopted, a critical issue in areas such as
sampling theory and statistics in medicine.
INFO: http://pow2.sta.uniroma1. it/tardella/workshop
Conference on Bayesian Applications and Methods in
Marketing. November 18-20, 1999. Fisher College of
Business, Ohio State University, Columbus, USA.
Bayesian methods offer a means of more fully understanding
issues that are central to marketing by
allowing researchers to build integrated models of behavior
that can be estimated with limited amounts of data.
The conference will bring together leading practitioners and scholars
in marketing who use Bayesian statistical
methods. The intent of the meeting is fourfold:
to provide training to students, practitioners, and academic researchers
on both basic and new Bayesian techniques;
to discuss current problems faced by practitioners and
data that are available for solving these problems;
to discuss new marketing methods and models;
to expose researchers in marketing to new advances
in Bayesian methods.
The conference is being sponsored by a number of different firms who offer
hierarchical Bayes software and
consulting services to their clients.
INFO: http://www.cob.ohio-state. edu/Bayes
Fifth Brazilian Meeting on Bayesian Statistics.
December 9-11, 1999. State University of Campinas (UNICAMP),
SP, Brazil.
The following topics will be explored: mixture models, MCMC
methods, stochastic processes and time series. The deadline for
submission of contributed papers and for two plenary
poster sessions is September 20, 1999.
INFO: mail to Jorge Alberto Achcar (Jorge@icmc.sc.usp.br)
228 Internet Resources
Software reviews. A lot of free and commercial
software for teaching and research is
available these days and many packages implement Bayesian methods.
The software reviews that appeared
in Maths&Stats (a quarterly newsletter published jointly
by the CTI centres in Birmingham and in Glasgow) are archived
at the CTI Statistics web site.
URL: http://www.stats.gla.ac.uk/cti/
ISBA Newsletter, June 1999 NEWS FROM THE WORLD
A web site for statistical computation. VassarStats is a
JavaScript-based site for statistical computation located at
Vassar College, Poughkeepsie, New York, USA. Basic frequentist
statistical methods have been implemented, but a Bayes' Theorem
calculator is also present. Most methods are accompanied by
a clear description of the background or by relevant references.
This resource is likely to be useful to students or to anyone
who wants to review his or her ideas with
the help of numerical examples.
URL: http://faculty.vassar.edu /~lowry/VassarStats.html
228 Miscellanea
Indian Chapter of the ISBA. The Indian Chapter of the
ISBA publishes a regular newsletter. If you are interested you can
contact Dr. S.K. Upadhyay (sku@banaras.ernet.in).
Imprecise probability models. The Journal of Statistical Planning
and Inference is to publish a special issue on the topic of imprecise
probability models and their applications.
The issue will include some of the papers that were presented at the First
International Symposium on Imprecise Probabilities and Their Applications
(ISIPTA '99), held in Ghent, Belgium, from June 29 to July 2, 1999.
The Journal will also consider additional submissions made before
September 22 on the following topics: statistical applications of
possibility theory, evidence theory, credal
sets, or related models; statistical inference based on prior ignorance;
studies of the foundations of statistics using imprecise probability
models; robust Bayesian methods; frequentist studies of robustness using
Choquet capacities or interval-valued probabilities; and innovative
statistical methods using imprecise probabilities. People interested
in submitting a paper should contact Peter Walley (walley@usp.br)
preferably before June 24.
International Workshop on Objective Bayesian Methodology.
June 10-13, 1999. València, Spain. There will not be
published proceedings, but authors were asked to place their papers
on their web sites. Pointers to these will appear on the workshop
web site http://www.uv.es/~bernardo/ workshop.html, and
some of them are already available.
Workshop on Expert Judgement, a review (by Roger M. Cooke).
June 21-24, 1999. Alphen-on-the-Rhine, Holland.
On June 21-24 the Technical University Delft (TUD) together with the
Forschungszentrum Karlsruhe (FZK), the National Radiological Protection
Board (NRPB) and Institut de Protection en de Sûreté
Nucléaire (IPSN) held a workshop on expert judgement and accident
consequence uncertainty analysis for nuclear power plants. The workshop
reported on research contracted by the European Commission, and the US
Nuclear Regulatory Commission, consisting of a stuctured expert judgement
assessment of uncertainties on modelling parameters for US and European
accident consequence models, and a calculation of uncertainties over model
endpoints. Participants from 22 countries, including Japan, Australia and
the US, attended the workshop.
The first two days were devoted to expert judgement methods.
Speakers from the US and European teams
focused on methods for selecting and
training experts, performance measures, performance based weighting, dependence
modelling, and probabilistic inversion.
The last two days consisted of feeding back results from the expert
judgement study to the experts themselves, and discussing overall results
of the uncertainty analysis. As a general conclusion, the method of
structured expert judgment leads to Bayesian confidence bands which
are significantly wider than the spreads of published ``best guesses''.
Eight expert judgement panels were conducted, and the results together
with expert rationales are published as EUR and NUREG reports.
Soon to
appear as EUR reports are uncertainty results for the European accident
consequence models, a procedures guide for structured expert judgement, and
a report on methodology, including performance weighting, dependence
modelling and probabilistic inversion.
Information on these publications
is available from Louis Goossens (louis.goossens@wtm.tudelft.nl).
ISBA Newsletter, June 1999
ISBA OFFICERS
Executive Committee
President: John Geweke
Past-President: Susie Bayarri
President-Elect: Philip Dawid
Treasurer: Valen Johnson
Executive Secretary: Michael Evans
Board Members
Mark Berliner, Enrique de Alba, Petros Dellaportas, Alan Gelfand,
Ed George, Jayanta Ghosh, Malay Ghosh, Jay Kadane, Rob Kass,
Daniel Peña, Luis Pericchi, Sylvia Richardson
Web page: http://www.bayesian.org/
EDITORIAL BOARD
Editor
Fabrizio Ruggeri <fabrizio@iami.mi.cnr.it>
Associate Editors
Bayesian Teaching
Jim Albert <albert@math.bgsu.edu>
Students' Corner
Sudipto Banerjee <sudipto@stat.uconn.edu>
Applications
Sujit Ghosh <sghosh@stat.ncsu.edu>
Software Review
Gabriel Huerta <gabriel@bayes.stats.nwu.edu>
News from the World
Antonio Pievatolo <marco@iami.mi.cnr.it>
Interviews
David Rios Insua <d.rios@escet.urjc.es>
Michael Wiper <mwiper@est-econ.uc3m.es>
Annotated Bibliography
Siva Sivaganesan <siva@math.uc.edu>
Corresponding Editors
Carmen Armero <carmen.armero@uv.es>
Marilena Barbieri <marilena@pow2.sta.uniroma1.it>
Christopher Carter <imchrisc@ust.hk>
Roger M. Cooke <r.m.cooke@twi.tudelft.nl>
Petros Dellaportas <petros@aueb.gr>
Eduardo Gutierrez Peña <eduardo@sigma.iimas.unam.mx>
Robert Kohn <robertk@agsm.unsw.edu.au>
Jack C. Lee <jclee@stat.nctu.edu.tw>
Leo Knorr-Held <leo@stat.uni-muenchen.de>
Udi Makov <makov@rstat.haifa.ac.il>
Marek Meczarski <mecz@sgh.waw.pl>
Renate Meyer <meyer@stat.auckland.ac.nz>
Suleyman Ozekici <ozekici@boun.edu.tr>
Wolfgang Polasek <wolfgang@iso.iso.unibas.ch>
Raquel Prado <raquel@cesma.usb.ve>
Josemar Rodrigues <josemar@icmc.sc.usp.br>
Alfredo Russo <arusso@unq.edu.ar>
Daniel Thorburn <daniel.thorburn@stat.su.se>
Antonia Amaral Turkman <antonia.turkman@cc.fc.ul.pt>
Brani Vidakovic <brani@stat.duke.edu>
Hajime Wago <wago@ism.ac.jp>
Simon Wilson <swilson@stats.tcd.ie>
Lara Wolfson <ljwolfson@byu.edu>
Karen Young <mas1ky@ee.surrey.ac.uk>
Mailing address: ISBA NEWSLETTER - CNR IAMI - Via Ampère 56 -
20131 Milano (Italy)
E-mail: isba@iami.mi.cnr.it Phone: +39
0270643206 Fax: +39 0270643212
