In Bayesian statistics the distinction between parametric and nonparametric methods refers to inference problems in which one can assume the existence of a true, but unknown, distribution for the random elements associated with the observations. If X is the set of all possible values of observations and M is the family of all possible distributions on X (including the true one, obviously) then the prior distribution, typical of the Bayesian paradigm, is a probability law 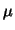on a 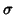-algebra of subsets of M. 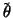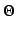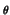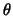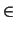Usually, the statistician's knowledge leads him/her to the definition (possibly unaware) of a function from M onto and a family of distributions M = {p : 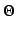} such that 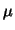({p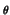}| 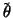= 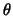) = 1 for any 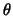in 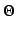. In other words, 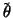plays the role of a sufficient statistical parameter: given the value of 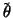, say 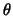, any further information is useless in determining the true law (assumed, in that case, coincident with p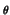). Usually, 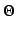is a subset of a Euclidean space, whose dimension is relatively small, and, therefore, it is convenient to implement the Bayesian paradigm on both the (prior) distribution on 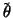and the statistical model M . As obvious, the statistical methods based on that approach are called parametric, whereas the term nonparametric refers to those methods in which 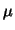is defined directly on M, without the intermediate use of parameters. Though more inherent to the Bayesian paradigm than the parametric formulation, the nonparametric one has attracted the interest of Bayesian only after the classical work A Bayesian analysis of nonparametric problems by Thomas S. Ferguson, published in the Annals of Statistics in 1973. An explanation for the late interest rests upon the conceptual difficulty in determining a distribution on M and the practical difficulty in defining and dealing with prior distributions on infinite dimensional spaces.

Historically, the nonparametric viewpoint goes back, at least, to the famous paper La prévision ses lois logiques, ses sources subjectives by Bruno de Finetti, published in the Annales de l'Institut Henri Poincaré in 1937, which contains a series of lectures given by the author at that Institute in May 1935. More precisely, the fundamental representation theorem of exchangeable laws itself is presented in a nonparametric form: a sequence of real-valued random variables is exchangeable if and only if its probability distribution can be represented as 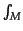p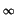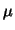(dp) for an adequate choice of 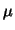. The theorem, as given by de Finetti, and its proof, although the natural extension of the already known result for events, were a cumbersome task in 1935-1937. It is noteworthy that de Finetti fulfilled that task, because of a convenient metrisation of M and an adequate definition of the integral on M, which came, at least, twenty years before the appearance of the general theory of weak convergence on metric spaces, due to Yuri V. Prokhorov.

A more direct link to the modern concept of Bayesian nonparametric statistical method can be found in a short note presented by de Finetti in 1934 at the XXIII meeting of the Società Italiana per il Progresso delle Scienze, published in 1935 with the title Il problema della perequazione [reprinted in Bruno de Finetti, Scritti (1931-1936), Pitagora Editrice, 1991]. In that paper the author shows, in a clear but very concise form, that the problem of fitting observations [loose translation of ``perequazione''] can be conceptually solvable by means either of a technique based on a nonparametric Bayesian estimation of the true law (the estimator being a mean value of the posterior distribution on M) or the predictive distribution of a future observation. The major flaw in the paper by de Finetti consists of the actual lack of examples of distributions on M which can show the practical implications of his ideas and be ``useful'' from a statistical viewpoint. Such goals were achieved only four decades later when Ferguson studied the extension of the Dirichlet distribution to M and analysed its application in Statistics.
Return to the main page