THE ISBA NEWSLETTER
Vol. 6 No. 1 March 1999
The official newsletter of the International Society for Bayesian
Analysis
 Return to the main page
Return to the main page
E-mail to the Editor:
isba@iami.mi.cnr.it
 Return to the top
Return to the top
A WORD FROM
THE PRESIDENT
by John Geweke
ISBA President
geweke@bayes.econ.umn.edu
It is fitting to begin this issue of the ISBA Newsletter with thanks to the previous editor, Mike Evans, for a job very well done. In particular, Mike served on an ad hoc basis, taking on tasks above and beyond the call of his position as ISBA secretary. All hail! It is just as fitting to thank the new editor, Fabrizio Ruggeri, for the energy and leadership that are evident everywhere in this new and reorganized Newsletter. This issue is just great, and gives promise of great things to come.
Since this is my first "word" as President, I reviewed the ISBA mission statement, which is at the
ISBA home page.
It begins, "ISBA was founded in 1992 to promote the development and application of Bayesian statistical theory and methods useful in the solution of theoretical and applied problems in science, industry and government. By sponsoring and organizing meetings and other activities the ISBA provides a focal point for those interested in Bayesian inference and its applications." This Newsletter provides lots of information about the meetings and activities of ISBA - in particular, the quadrennial world meeting of ISBA in Crete in May, 2000.
The ISBA mission statement focuses on developing solutions to real problems. I have always found this focus to be very fruitful in my primary academic field of economics. An audience of economists, even an audience of econometricians, will often go to sleep if the main topic is the weak sufficiency principle, Lindley's paradox, or the latest nuance in Markov chain Monte Carlo methodology. (If one is lucky. One can produce outright hostility given a little effort.) That same audience, if presented with the solution of a real, applied, problem, will sit up and take notice. The more important and common is the problem, the greater will be the interest. In my experience the fact that the solution involves Bayesian methodology is of at most secondary interest, the first time an economist encounters a Bayesian approach. But as the experience is repeated, econometricians and other methodologically inclined economists naturally seek out the common denominator, and for some this
leads to serious study of the weak sufficiency principle, Lindley's paradox, and so on. Many will never take this step: they are practical people looking for solutions that work, and are happy to apply them without plumbing the depths of methodology. I have always thought that this reaction by practical people is the ultimate recognition of the utility of Bayesian methods.
As you look at this issue of the Newsletter you will see, alongside the stories of meetings and events,
indications of this practical success of Bayesian methods.
I call your attention in particular to the article on the Ph.D. thesis by Patrick Bajari,
"The First Price Auction with Asymmetric
Bidders: Theory and Applications," which won the Zellner Award in 1997. The Zellner award is given by the editorial board of the Journal of Business and Economic Statistics to the best thesis in economics and statistics each year. The award is not for the best Bayesian thesis, and the committee is not comprised of Bayesians. Bajari's thesis makes advances in economic theory and applies them to the practical problem of designing bidding systems for road repair contracts so as to reduce expenditures by local governments. Theory and data meet through Bayesian inference using applications of recently developed MCMC methods. The focus of the thesis is not Bayesian, but the problem could not be solved with non-Bayesian methods. Many economists have take
notice! Through the repetition of this sort of success, Bayesian methods will spread in science.
As always, update my posteriors at geweke@bayes.econ.umn.edu.
 Return to the top
Return to the top
A WORD FROM
THE EDITOR
by Fabrizio Ruggeri
ISBA Newsletter Editor
fabrizio@iami.mi.cnr.it
Starting with this issue, you will see a completely new ISBA
Newsletter (NL), with a new Editor and, for the first time in its history,
an Editorial Board. The NL is the result of the efforts of many people:
Associate and Corresponding Editors (see their names in the last page),
those who contributed a column to the issue, many of you who discussed a
proposal for the ``new'' NL and gave valuable suggestions, the ISBA officers,
my colleagues at IAMI, the staff at ISDS. I wish to thank all of them.
Now it is your turn. We are looking forward to receiving your comments
and contributions to the NL. A section on Letters will be started as
soon as we get any. Moreover, the Associate Editors will be happy to consider
your suggestions for topics to be covered in future issues.
I am looking forward to getting your feedback on the NL, suggestions and
criticisms, proposals for new sections (e.g. Book reviews).
We would like the NL to become a valuable source of
information and a place for discussion.
Nowadays, news on conferences, prizes, etc. is spread very
quickly through Internet. It makes little sense to have a NL focusing just on
this type of information though we do plan to have a news section (News
from the world),
in which a short presentation of the facts will be followed by an e-mail or
a web address. At the same time, we do not plan to become a
scientific journal: this is not the purpose of a NL. We will though have a
section on Bayesian History, where little known facts will be
brought to the knowledge of a larger audience, stimulating, hopefully,
further reading on those topics. In this issue Prof. Regazzini presents a
little known paper on Bayesian nonparametrics by de Finetti.
The past, present and future of Bayesian statistics will be discussed
by leading Bayesians in the section on Interviews: we start with
Prof. Zellner; a quite natural choice as one of the founding members of ISBA!
Dissemination of Bayesian ideas
is, of course, important. This starts from the courses that many of us
are teaching. The section on Teaching will be a place where teaching
experiences and tools are discussed. Dissemination is possible also if Bayesian
methods are successfully applied to real problems: a section on Applications will describe some key Bayesian contributions.
The sections on Software and Bibliography should help researchers
by pointing out new software and providing references on promising, but less
well known fields.
We also provide a section for Bayesians of the future. A Ph.D. student is in
charge of the Students' corner, where students can discuss
issues of common interest. In this issue we present abstracts of Ph.D.
dissertations discussed in 1998 at ISDS, Duke University. We encourage
Departments to send us abstracts of their Ph.D. dissertations.
We would like to spread information about Bayesian
activities in countries
where the use of Bayesian ideas is a quite recent phenomenon: we start with
Venezuela and we learn how the local Bayesian group started and grew.
We have not forgotten that our NL is the ``official newsletter'' of ISBA; thus
readers will find news on the ISBA's activity too.
In this issue, we
start with the call for session organisers and papers for ISBA 2000, the
6th world meeting of ISBA.
A final word about the NL and its Editorial board: the Associate Editors (AE)
have been appointed for a two-years term (except the AE of the Students'
corner who has to write his dissertation!), whereas the Corresponding
Editors's term lasts one year to get a larger number of ISBA members
involved in the NL. The NL will be published 4 times a year. In early
messages sent to bayes-news and ISBA members, we asked people to tell us
if they wanted the NL by e-mail. Because of the small number of answers,
we have decided, for the moment, to mail the NL to all the ISBA members.
In a future we might think again of an electronic delivery.
This issue is sent to all the Bayesians (and non Bayesians) who have
requested it, regardless of their membership in ISBA. We hope that
most of them will take the little step to fill the form at the end of
the NL, turn it in to Prof. Valen Johnson and become part of ISBA
(and get the next issues of the NL, as well ...)
 Return to the top
Return to the top
Call for session organisers and papers
ISBA 2000
The 6th World Meeting of the International Society for Bayesian Analysis
Hersonissos, Crete
May 28-June 1 2000
The 6th World Meeting of ISBA will take place in Crete between May 28 and
June 1 2000. ISBA is pleased to announce participation and co-sponsorship
from EUROSTAT and from the Association of Balkan Statisticians.
The Scientific Committee solicits proposals from individuals interested in
organising sessions, and also from authors of individual papers. A major
focus of the meeting is Bayesian methods in government, official statistics
and public policy, and several sessions will be reserved for presentations
on topics related to the theme. Beyond this, the meeting will feature sessions
on research and applications of Bayesian statistics in many diverse areas,
especially on topics consistent with the interdisciplinary outlook and mission
of ISBA. Talks will be organised in sessions of 2 or (mainly) 3 presentations,
each talk being 30 minutes long, including discussion time.
We invite proposals from
 session organisers interested in putting
together a session of 2 or 3 talks on a specific topic
session organisers interested in putting
together a session of 2 or 3 talks on a specific topic
 contributing speakers on any topic.
contributing speakers on any topic.
We particularly encourage
proposals in areas related to the meeting theme.
Suggested session topics are listed below, though proposals need not be
restricted to these areas.
Possible Theme topics:
 Bayesian methods and official statistics
Bayesian methods and official statistics
 Statistics in the European Union
Statistics in the European Union
 Bayesian statistics in national and international finance
Bayesian statistics in national and international finance
 Confidentiality and disclosure limitation
Confidentiality and disclosure limitation
 Economic and governmental forecasting
Economic and governmental forecasting
 Government accounting and/or auditing
Government accounting and/or auditing
 Risk assessment (environmental, economic/business, etc)
Risk assessment (environmental, economic/business, etc)
 Bayesian methods in insurance
Bayesian methods in insurance
 Bayesian methods in agriculture
Bayesian methods in agriculture
 Decision analysis in government policy
Decision analysis in government policy
 Statistics in education and education policy
Statistics in education and education policy
 Bayesian methods in political science
Bayesian methods in political science
 Bayesian methods in sampling and census, including non-response
in surveys
Bayesian methods in sampling and census, including non-response
in surveys
 Bayesian statistics in public health (disease mapping, health
care policy, program evaluation, etc).
Bayesian statistics in public health (disease mapping, health
care policy, program evaluation, etc).
Under the general theme of government and official statistics, we solicit
proposals for one or more formatted sessions with two or three speakers
presenting a coordinated discussion of important statistical and societal
problems. Such a session might involve a subject matter expert to present
the problem and background work, followed by one or two speakers discussing
specific Bayesian approaches and contributions, highlighting challenges
and unsolved problems, and possibly discussing advantages of Bayesian
methods over earlier (Bayesian and non-Bayesian) approaches.
In addition to the theme topics, we encourage proposals for sessions and talks
in any area of Bayesian statistics and decision science, including
topics in theory, methodology and applications.
Proposals from session organisers must include the names of proposed speakers
(preferably 3 speakers) and a session chair. Proposers of such sessions will
assume responsibility for managing the speakers and ensuring a successful
session at the meeting. Tentative titles of all talks should be included
with the names of proposed speakers. Individual authors should simply send
a proposed title for their talk. All proposals should include full e-mail
addresses of all named participants, as well as their institutional
affiliations.
All individuals interested in presenting at the meeting will be able to do so,
in either a plenary or parallel session of talks, or in evening poster
sessions.
Individuals who prefer to present in a poster session should mention that on
their submission.
All proposals should be e-mailed to Mike West, and all future correspondence
with the Scientific Committee will be carried out electronically. Enquiries
can be e-mailed to any member of the Scientific Committee. To be given full
consideration, proposals for sessions or for individual talks must be
received no later than October 1, 1999. While we will accept proposals
that are received later than the October 1 deadline, we cannot promise
that all organizers' requests will be met.
This call for participation, and other details of ISBA 2000, is available
at the ISBA web site.
under the Meetings link.
ISBA 2000 Scientific Committee
Alicia Carriquiry,
Iowa State University, Ames IA, USA
alicia@iastate.edu
George Kokolakis,
National Technical University of Athens, Greece
kokolakis@math.ntua.gr
Daniel Peña,
University Carlos III, Madrid, Spain
dpena@est-econ.uc3m.es
Gilbert Saporta,
Conservatoire National des Arts et Metiers, Paris,
France
saporta@cnam.fr
Adrian Smith,
Queen Mary and Westfield College, London, UK
afms@qmw.ac.uk
Mike West
(Committee Chair),
Duke University, Durham NC, USA
mw@stat.duke.edu
 Return to the top
Return to the top
ARNOLD ZELLNER
by Michael Wiper
mwiper@est-econ.uc3m.es
Professor Zellner is a founding member of ISBA and was president of ISBA
in 1994-1995. ISBA gave him a Founder's Award Plaque in 1998. Professor Zellner
was President of the American Statistical Association (ASA) in 1991, first
Chair of the ASA Section on Bayesian Statistical Science in 1993 and
Seminar Leader of the NBER-NSF Bayesian Seminar for 25 years.
He has worked at the University of Chicago since 1966 and is Distinguished Service Professor
Emeritus of Economics and Statistics. He has worked in Bayesian
statistics and economics for more than 30 years and has published more
than 200 articles, monographs and books, many of which have been
extremely influential in Bayesian research. He has received numerous
awards and worked with statisticians and economists all over the world. A
fuller description of his work can be seen
at his
homepage.
We e-mailed Professor Zellner a number of questions about his career
and the Bayesian world in general. Here are his responses.
1. Why did you decide to become a statistician?
After getting an undergraduate degree in physics at Harvard, I
completed about a year and a half of graduate work in physics at U. of
California at Berkeley where I interacted with my brother Norman and his
friends who were doing doctoral work in quantitative economics. I
became
aware of a great opportunity to develop and use quantitative methods and
data to solve economic and business problems. I have been pursuing
these
objectives for many years and have come to view methods for learning
from
data and making decisions, that is statistics, as the foundation of all
the
sciences.
And why Bayesian?
Since reading Sir Harold Jeffreys's books in the 1960s, I was
impressed by the central role that his
axioms and successful applied studies gave to Bayes's Theorem and uses
of
it in estimation, testing, prediction, etc. Thus, I started a program
of
research to compare Bayesian and non-Bayesian statistical solutions to
various problems. Over the years, I and others found that Bayesian
solutions were generally better and thus I and many others were happy to
become identified as BAYESIAN.
2. Can you name some of the people and events that have had a
great
influence on you during your career?
In addition to interaction with my PhD. thesis advisors George
Kuznets, Ivan Lee and Robert Gordon, who were very helpful,
interaction with George Box in the 1960s when I was a faculty member at
the U.of Wisconsin was very stimulating given his deep understanding of
statistical theory and application. Then too, Sir Harold Jeffreys's work
and comments were and are extremely influential with respect to my
theoretical and applied Bayesian work. Jeffreys's philosophy,
simplicity
postulate, invariant priors, information theory measures, and
applications
had an extremely important influence on me and my work. On the several
occasions when I visited with Jeffreys at Cambridge, our conversations
were
most constructive. The same can be said with respect to many
interactions
with George Barnard and Jack Good. Both offered constructive comments
and
helpful references on many occasions.
In addition, it was Barnard and
Jenkins' JRSS paper in the 1960s on a "weighted likelihood" approach to
the
analysis of time series models that led me to view the weighting
function
as a prior density and to realize that this then produced exact finite
sample inferences for time series models...no asymptotics
needed!!!! What a lovely realization that was.
Then too, George Barnard
and Edwin Jaynes have been very constructive in the late 1980s and 1990s
in connection with my derivation of optimal information processing
rules, including Bayes's Theorem,
and my development of the Bayesian method of moments (BMOM) that yields
inverse probability statements regarding parameters and future
observations without the use of a likelihood
function and Bayes's Theorem.
We have now tested, using post data odds,
BMOM and traditional Bayesian predictive densities using data,
a procedure that appealed very much to George Barnard.
Last I have been very fortunate to have had many able
colleagues and graduate students work with me on my NSF grants from the
1960s to the present, many of whom co-authored papers with me (see
papers listed on my homepage.)
Our hard work and
long discussions were very influential in shaping my thoughts as were
the
many comments received at semi-annual meetings of the NBER-NSF Seminar
on
Bayesian Inference from 1970 and thereafter.
While at the U. of Chicago since
1966, the following past and present colleagues have been very influential
and helpful: Milton Friedman, Ed George, Al Madansky, Rob McCulloch, Jim Press,
Harry Roberts, Peter Rossi, Steve Stigler, Hodson Thornber, George Tiao and
David Wallace.
3. Modesty apart, what do you consider to be your own
contribution to statistics?
Modesty apart, I believe that I have done much through my research, teaching
and other efforts to have the Bayesian approach be accepted in
statistics and econometrics. Working many
problems from several points of view and comparing solutions, mentioned
earlier, has been a particularly effective approach.
Further, I take great pride in my work on seemingly
unrelated regression models (SURs) that have been very useful in many
fields. Then, immodestly, I believe that the optimal information
theoretic
maximal data information priors (MDIPs) that can, with appropriate side
conditions, be made invariant to relevant transformations are extremely
useful. Then producing an optimal information processing procedure that
yields Bayes' Theorem as a 100% efficient information processing rule
and a
first relation between Bayes's Theorem and entropy,
as noted by Ed Jaynes, appears important to me. Also, employing this
approach with other inputs has produced new, optimal information
processing rules. Next, I have
produced a whole range of minimum expected loss (MELO) estimates and
point
predictions for many problems, balanced loss functions, solutions to
many
applied problems including point and turning point forecasting,
portfolio
problems, control problems, etc. And most recently, there is
the Bayesian method of moments (BMOM) that has been applied to many
different models and problems and permits Bayesians to make inverse
probability statements when the form of the likelihood function is
unknown.
Last, and very important,
I take great pride in having worked with a large number of doctoral
students over the years who have produced remarkable
theses, most of them Bayesian, and gone on to have very successful
careers in research, teaching and consulting in the U.S. and many other
countries.
And what is your "best" piece of work?
Given my prejudices, I would have to say my book, An Introduction to
Bayesian Inference in Econometrics, Wiley, 1971,
reprinted in Wiley Classics Library, 1996. It was an early report on
the
usefulness of Bayesian inference and provided many
examples comparing Bayesian and non-Bayesian solutions to estimation,
prediction, testing and control problems. Many different models,
including
my seemingly unrelated regression (SUR) model, were analyzed and
examples
computed. Much of my later work was done to extend and improve analyses
that appeared in this 1971 volume, including work on estimating reciprocals,
ratios, structural coefficients, and other functions of parameters in the
MELO approach, extending
the MDIP approach to producing priors, introducing
broadened, "balanced" loss functions, etc.
4. Have you ever experienced any discrimination against
Bayesianism?
No. The best that I can provide along these lines is a remark
that Ted Anderson made at his 80th birthday party last June when I said
he looked more like 40 than 80. He replied that
you Bayesians never could count. Also, Jim Durbin once remarked that
genetics determines who is Bayesian and who is
not Bayesian. A few years later, he presented a Bayesian paper at a
seminar at the U. of Chicago. I remarked that his
genes must have changed. He remarked, "What's all this fuss about a
little mathematics?"
5. For students starting out, would you recommend them to go
into Bayesian statistics and, if so, what advice would you give them?
By all means I would tell them to learn Bayesian statistics and make
sure that in their courses and work that they work inference and
decision
problems from different points of view and compare
solutions. To make meaningful comparisons, they have to understand not
only the Bayesian approach but others, e.g. sampling, likelihood, structural,
empirical likelihood etc.
approaches. In recent lecturing to grad students, I have found that many
coming into my courses are all
mixed up about definitions of probability, interpretations of Bayesian
and non-Bayesian confidence and prediction intervals, testing
procedures,
etc. In an old fashioned approach to get them straightened out, I tell
them that these and similar issues will be featured on the final
examination. Then they get serious and learn what's what.
6. Having worked with economists for many years, do you find
their views about
Bayesian methods as a whole to be different from workers in other
fields, e.g. physicists, engineers etc?
Economists, in contrast to workers in other fields, tend to be more
familiar with the theory of
decision-making under uncertainty developed by Ramsey, Savage, Friedman
and others. Also, economic theorists have used
Bayes's Theorem as a learning model for many years. However, many older
quantitative, applied economists and econometricians have just received
non-Bayesian material in their training and many tend to be wary of the
Bayesian approach
using arguments that have appeared in old statistics and econometrics
texts. However, the new generation is much better educated in Bayesian
matters and has already produced many important and useful Bayesian
results. With respect to
physicists, many, if not most, are not well-trained in statistics,
Bayesian or non-Bayesian. Surprisingly, not very many physicists with
whom
I have come into contact have read Jeffreys's book, Theory of
Probability,
although more tell me that they
will read it. Many engineers have taken courses in engineering
statistics
and appear to me to be quite pragmatic. They will use
anything that works in practice, including Bayesian analysis, perhaps
prodded along by Richard Barlow who teaches engineers
Bayesian analysis at the U. of California at Berkeley.
7. What do you enjoy most about your work?
Getting solutions that work well in practice and seeing grad
students succeed in their doctoral research and careers.
And least?
Grading examinations and attending "windy'" academic committee
meetings.
8. What is your favourite statistics book?
H. Jeffreys's, Theory of Probability [Note that physicists tend to
refer to statistics as "probability theory," perhaps because Rutherford
is supposed to have
said that if you need statistics to analyze your data, your experiment
needs redesigning.] I also like Jim Berger's book,
Statistical Decision Theory and Bayesian Analysis, 2nd ed.
Springer-Verlag, 1985.
9. What is your favourite Bayesian statistics joke?
Would you want your daughter to marry a Bayesian?
10. Why did you decide to start ISBA?
Bayesian statistics had become so important as a foundation for all
the sciences that many, including myself, thought it appropriate to aid
its
development world-wide by creating ISBA. In addition, our NBER-NSF
Bayesian
Seminar group had had many productive and very enjoyable meetings in
Venezuela, Mexico, India, Canada, Brazil, etc. and thus the decision
to extend these interactions into the
future in a more organized manner was not hard.
What do you think about ISBA now after 6 years?
ISBA's growth and development, particularly its successful meetings,
new chapters in India, Chile and S. Africa, and enlarged membership are
very impressive. Also, I particularly like the plans for the new,
expanded
ISBA Newsletter that have recently been circulated worldwide. The new
Newsletter, it appears to me, will be one step along the way to a much
needed ISBA Journal of Bayesian Analysis serving all the disciplines.
How should ISBA develop over the next few years? Are
there any
specific things you would like to see it do?
While there are many possibilities, including the production of an
ISBA Journal of Bayesian Analysis, I would like to see ISBA do all it
can to support the
activities, meetings and publications of the Chapters, new and old.
With respect to world meetings, it would also
appear worthwhile to have volumes produced that
contain the major theoretical and applied papers and general discussions
of major issues presented at each meeting. If well-designed and if many
relevant issues are treated, e.g. how to use Bayesian analysis to make
tax
and budget policy as done by
Charles Whiteman in connection with his consulting with the governor of
the State of Iowa, these volumes may become "best
sellers" and generate revenue for ISBA and its Chapters.
11. What have been the greatest changes in Bayesian methods in
the years since you started?
One is the current ability to compute almost any integral by numerical
techniques, e.g. MCMC, etc.
Second, we now have a plethora of procedures for producing both diffuse
and informative priors. Third, and very important, we now have many
more
successful applications of Bayesian analysis, e.g. Mike West's
impressive
applied work, Jose Quintana's
and Blu Putnam's very useful Bayesian portfolio formation
applications,
etc. Now we not only have good theory, we also have
impressive performance in practice to which we can point.
Are all these changes for the good or has anything been
lost?
I can't think of anything that has been lost by experiencing these
remarkable, valuable changes.
12. What do you predict will be the changes in the next 10 years
of Bayesian statistics?
Forecasting 10 years into the future is very difficult.
Hence take the following with a few grains of salt.
While Bayes' Theorem has been a valuable learning model for workers
in all the sciences, as with all models, the
Bayesian learning model will probably be generalized and changed in
certain ways. Then work to evaluate the modified versions will be
undertaken. Work by Diaconis, Zabell, Goldstein and myself has already
resulted in new learning models that are in the
process of being evaluated which should make Bayesian learning
applicable
to a broader range of problems and even more effective than it is today.
After all, the Model-T was followed by the Model-A, the V-8 Model, etc.,
Newton's Laws by Einstein's Laws, etc.
13. Are we headed for a Bayesian millennium?
In my article, A Bayesian Era, read at a Valencia meeting and
published in
the 1988 volume, Bayesian Statistics 3, ed. J.M. Bernardo et al, I
stated that a Bayesian Era has already started. Subsequent developments
including the founding of ISBA and of the ASA Section on Bayesian
Statistical Science in 1992 and the strong upsurge in the number of
Bayesian papers and publications world-wide would lead me to say,
immodestly, that I was right.
Also, the benefits to society of having Bayesian statistical methods
that
are sound and that yield good solutions to inference, decision and
control
problems are enormous and deserve to be measured and reported.
Congratulations to all of us who have helped make this Bayesian Era
come
into existence.
If you would like to read more about Professor Zellner's career, you can
see another interview with him in the journal, Econometric Theory, 5,
1989, 287-317
which is reprinted in Professor Zellner's book Bayesian Analysis in
Econometrics
and Statistics: The Zellner View and Papers, Edward Elgar Publ. Ltd,
1997. There is also an interesting collection of 48 papers by 98 authors in honour of
Professor Zellner:
Bayesian Analysis in Statistics and Econometrics: Essays in Honor of
Arnold Zellner, edited by Donald A. Berry, Kathryn M. Chaloner and John K.
Geweke, Wiley, 1996.
 Return to the top
Return to the top
BAYESIAN
NONPARAMETRICS
by Eugenio Regazzini
eugenio@iami.mi.cnr.it
We discuss early works on Bayesian nonparametrics due to
Bruno de Finetti.
In Bayesian statistics the distinction between parametric and nonparametric
methods refers to inference problems in which one can assume the existence
of a true, but unknown, distribution for the random elements associated
with the observations. If X is the set of all possible values of observations
and M
is the family of all possible distributions on X (including the true
one, obviously) then the prior distribution, typical of the Bayesian paradigm,
is a probability law 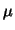 on a
on a 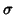 -algebra of subsets of M. Usually,
the statistician's knowledge leads him/her to the definition
(possibly unaware) of a function
-algebra of subsets of M. Usually,
the statistician's knowledge leads him/her to the definition
(possibly unaware) of a function
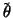 from M onto
from M onto 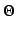 and a family of distributions
M = {p
and a family of distributions
M = {p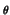 :
: 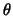
 } such that
} such that
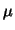 ({p
({p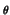 }|
}|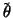 =
= 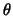 ) = 1 for any
) = 1 for any 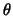 in
in 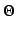 . In other words,
. In other words,
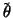 plays the role of a sufficient statistical parameter:
given the value of
plays the role of a sufficient statistical parameter:
given the value of
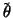 , say
, say 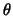 , any further information
is useless in determining the true law (assumed, in that case,
coincident with
p
, any further information
is useless in determining the true law (assumed, in that case,
coincident with
p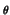 ). Usually,
). Usually, 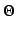 is a subset of a Euclidean
space, whose dimension is relatively small, and, therefore, it is convenient
to implement the Bayesian paradigm on both the (prior) distribution on
is a subset of a Euclidean
space, whose dimension is relatively small, and, therefore, it is convenient
to implement the Bayesian paradigm on both the (prior) distribution on
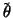 and the statistical model M
. As obvious, the statistical
methods based on that approach are called parametric, whereas the
term nonparametric refers to those methods in which
and the statistical model M
. As obvious, the statistical
methods based on that approach are called parametric, whereas the
term nonparametric refers to those methods in which 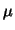 is defined
directly on M, without the intermediate use of parameters. Though
more inherent to the Bayesian paradigm than the parametric formulation,
the nonparametric one has attracted the interest of Bayesian only after the
classical work A Bayesian analysis of nonparametric problems by Thomas
S. Ferguson, published in the Annals of Statistics in 1973.
An explanation for the late interest rests upon the conceptual difficulty
in determining a distribution on M and the practical difficulty in defining
and dealing with prior distributions on infinite dimensional spaces.
is defined
directly on M, without the intermediate use of parameters. Though
more inherent to the Bayesian paradigm than the parametric formulation,
the nonparametric one has attracted the interest of Bayesian only after the
classical work A Bayesian analysis of nonparametric problems by Thomas
S. Ferguson, published in the Annals of Statistics in 1973.
An explanation for the late interest rests upon the conceptual difficulty
in determining a distribution on M and the practical difficulty in defining
and dealing with prior distributions on infinite dimensional spaces.
Historically, the nonparametric viewpoint goes back, at least, to the famous
paper La prévision ses lois logiques, ses sources subjectives by Bruno
de Finetti, published
in the Annales de l'Institut Henri Poincaré in 1937, which contains
a series of lectures given by the author at that Institute in May 1935. More
precisely, the fundamental representation theorem of exchangeable laws itself
is presented in a nonparametric form: a sequence of real-valued random
variables is exchangeable if and only if its probability distribution can
be represented as
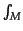 p
p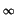
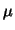 (dp) for an adequate choice of
(dp) for an adequate choice of 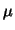 .
The theorem, as given by de Finetti, and its proof, although the natural
extension of the already known result for events, were a
cumbersome task in 1935-1937. It is noteworthy that de Finetti fulfilled
that task, because of a convenient metrisation of M and an adequate
definition of the integral on M, which came, at least, twenty years before
the appearance of the general theory of weak convergence on metric spaces,
due to Yuri V. Prokhorov.
.
The theorem, as given by de Finetti, and its proof, although the natural
extension of the already known result for events, were a
cumbersome task in 1935-1937. It is noteworthy that de Finetti fulfilled
that task, because of a convenient metrisation of M and an adequate
definition of the integral on M, which came, at least, twenty years before
the appearance of the general theory of weak convergence on metric spaces,
due to Yuri V. Prokhorov.
A more direct link to the modern concept of Bayesian nonparametric statistical
method can be found in a short note presented by de Finetti in 1934 at the
XXIII meeting of the Società Italiana per il Progresso delle Scienze,
published in 1935 with the title Il problema della perequazione [reprinted
in Bruno de Finetti, Scritti (1931-1936), Pitagora Editrice, 1991]. In
that paper the author shows, in a clear but very concise form, that the problem
of fitting observations
[loose translation of ``perequazione''] can be conceptually solvable
by means either of a technique based on a nonparametric Bayesian estimation
of the true law (the estimator being a mean value of the posterior
distribution on M) or the predictive distribution of a future observation.
The major flaw in the paper by de Finetti consists of the actual lack of
examples of distributions on M which can show the practical implications
of his ideas and be ``useful'' from a statistical viewpoint. Such goals
were achieved only four decades later when Ferguson studied the extension
of the Dirichlet distribution to M and analysed its application in Statistics.
 Return to the top
Return to the top
TEACHING BAYES TO BEGINNERS
by Jim Albert
albert@bgnet.bgsu.edu
Bayes in introductory courses and
future topics.
Generally, I think it is
safe to say that most people are introduced to statistical inference from a
frequentist perspective. Many students in graduate programs in statistics
are not taught the basics of the Bayesian paradigm including subjective
probability, the modeling of prior beliefs through probability
distributions, and posterior and predictive inference. This lack of
exposure of students to Bayesian thinking has had a major impact on the
growth of the use of Bayesian methods in areas of application. I think it
is important to discuss how we can effectively communicate Bayesian ideas
in academic and industrial settings and how we can facilitate the spread of
Bayesian thinking among applied statisticians.
This column will discuss a variety of issues relevant to teaching Bayesian
ideas. Here is a short list of some topics, although other suggestions by
ISBA members are certainly welcome.
 How can one introduce Bayesian thinking in the standard elementary
statistics class taught as a service course to non-math majors?
How can one introduce Bayesian thinking in the standard elementary
statistics class taught as a service course to non-math majors?
 Is it desirable to teach both Bayesian and frequentist thinking in an
introductory class?
Is it desirable to teach both Bayesian and frequentist thinking in an
introductory class?
 What topics should be taught in an introductory applied Bayesian course at
the graduate level?
What topics should be taught in an introductory applied Bayesian course at
the graduate level?
 What is the role of software in teaching Bayesian inference?
What is the role of software in teaching Bayesian inference?
 What are effective short courses for teaching Bayesian methodology?
What are effective short courses for teaching Bayesian methodology?
 How do we argue that Bayesian inference is superior (at least in some
settings) to frequentist inference?
How do we argue that Bayesian inference is superior (at least in some
settings) to frequentist inference?
In future columns, I hope to describe Bayesian courses that are currently
offered and give reviews of recently published texts and software that will
help in communicating Bayes.
Recently (August 1997) a series of articles appeared in the American
Statistician on the desirability of introducing Bayesian thinking in the
first introductory statistics class taught as a service course to students
outside of the mathematics or statistics department. I have taught
introductory statistics for over 20 years and I have found it very
difficult communicating frequentist thinking to this audience. The notion
of a sampling distribution is obscure to students and, more importantly,
the students have a hard time understanding the repeated sampling
interpretation of confidence. I think Bayesian thinking is very attractive
at this level. Thinking in terms of subjective probability is very natural
for students and Bayes rule can be taught as a formal mechanism for the
natural process of updating one's beliefs about unknowns when more
information is observed.
Currently Alan Rossman and I are writing a beginning statistics text that
introduces inference from a Bayesian viewpoint. The first half of the test
focuses on data analysis. The second half introduces probability basics
-- the focus is on the interpretation of discrete probability tables for
one and two variables. Inference is first introduced for categorical
models using Bayes rule. A two-way table, a ``Bayes box" (hypothetical
counts classified by models and data), is used to teach Bayes rule. We
then have chapters on inference for one and two proportions and a normal
mean. We focus on the use of discrete priors for unobservables, since
these are easier to assess and interpret and it avoids any use of calculus.
One innovative aspect of this text is that it essentially is a collection
of activities that students work on in class in small groups. Currently
we are using this material at Bowling Green for five sections a semester.
I think the course is successful in getting across the big ideas in
inference (population, samples, confidence in making inference) and the
student is well prepared to take a second statistics class on methodology.
Unfortunately, there are very few elementary statistics texts currently
available that use Bayesian thinking. One text of note is Don Berry's
text ``Statistics: A Bayesian Perspective". I have used Don's text both at
Duke and Bowling Green with success and I would recommend it for anyone who
is teaching a one semester introductory class. Don's text has been very
influential in my thinking about teaching elementary Bayes.
 Return to the top
Return to the top
TVAR MODELS
by Gabriel Huerta
gabriel@bayes.stats.nwu.edu
We review software, developed at Duke University,
for nonstationary time series analysis and decomposition
using time-varying parameter autoregressions.
This software provides Fortran 90-Splus functions and Matlab
programs to fit Time-Varying Autoregressive (TVAR) models with a fixed order
using a Bayesian Dynamic Linear Model (DLM) framework. The evolution
of parameters in time is defined through a Random Walk and with
standard Normal-Inverse Gamma priors on model coefficients and
variances. Using a DLM algorithm for sequential and
retrospective smoothing, the software computes posterior
estimates of the AR coefficients and variances at each time. The
main focus is on inference on latent component structure defined through the
time-varying characteristic roots of the process.
Basically, the
software is organised in three parts and particularly for the Fortran-Splus
version each one is defined as follows. A program named "grid.90",
computes the log-likelihood and mean square error (MSE) of a DLM-TVAR for a
desired grid of values for model order and discount factors for the
evolution of parameters. As output, the combination of order-discount
factors that maximises the log-likelihood and minimises the MSE are
reported and both can be used for further analysis. The second part consists of a program
named "tvar.90" which fits the TVAR model for any specification of
model order and discount factors. "tvar.90"
computes and saves posterior means for model parameters and has the
additional option of generating samples from the posterior distribution of
the parameters at each
time. Finally,
the program named "decomp.90", reads the output for "tvar.90" and
produces posterior inference on latent component structure with
component ordering via the amplitude, periodicity or corresponding moduli for
characteristic-component roots. Furthermore, the Splus functions summarise the
output of the Fortran programs offering different graphical displays.
Some involve plots of the data with the time-varying latent components, time trajectories for moduli and
frequency of the associated characteristic roots which can also include
95 % posterior intervals at selected time points.
The software is designed for a Unix environment and the Fortran
version requires LAPACK, public domain software for matrix algebra. On
the other hand, the MATLAB version is free-standing and permits
time-varying spectral inference. The software comes with
3 data sets and tutorial examples. The data sets are:
an Electro-Encephalogram (EEG) trace, an oxygen-isotope time series and a
series of non-stationary sea level pressures. Particularly
for the EEG data, the Matlab version offers the possibility of contour/surface
plotting of the EEG channels and related inferences over a graphical
representation of the head of a person. As the authors of the software
point out, the Matlab version requires further upgrading.
This a very general software for modelling time series within a linear-non
stationary context that incorporates model selection through a formal
likelihood exploration. Although all the emphasis is in latent structure
rather than aspects as forecasting, it offers a diversity of analysis
for component modelling that range from simple computation of posterior
moments to exploration via direct Monte Carlo simulation of posterior
distributions. Additionally, component structure can be studied with a variety of
orderings so properly handles for identifiability issues that
naturally arise in DLM-TVAR models.
The software is free, occupies approximately 99 Kb of disk space and
is available to the public domain from
web-site at which key-reference can also be found.
 Return to the top
Return to the top
1997 ZELLNER AWARD
by Patrick Bajari
bajari@leland.stanford.edu
The award is given by the editorial board of the Journal of Business and Economic
Statistics to the best thesis in economics and statistics each year.
Patrick Bajari's thesis, "The First Price Auction with Asymmetric
Bidders: Theory and Applications" uses new methods in economic theory and
Markov Chain Monte Carlo to tackle an old problem: developing an econometric
model of competitive bidding. Understanding competitive bidding is a
question of considerable practical importance. Worldwide, the construction
industry is a 3.2 trillion dollar market (Engineering New-Record, 11/30/98)
where a large percentage of contracts are awarded by some form of
competitive bidding. The particular market considered in his research was
bidding by construction firms in Minneapolis, Minnesota for contracts to
repair and build highways. The methodology, however, could be applied to
study bidding in other procurements. The research addressed three
questions. First, what is the (unobserved to the econometrician) cost
structure of each firm in the market. Second, what is the posterior
probability that the market is competitive or collusive. Third, what are
the econometrician's posterior beliefs about bidding if different rules were
used in awarding the contracts.
Bayesian methods are well suited to study these problems. After
considerable research into the cost structure of the market, the author was
able to develop restrictions on the space of parameter values in the firm's
cost structures. The prior had compact support, that is, some parameter
values were given zero prior probability (a trivial example is that trucking
costs should not be negative and can be bounded above by using market prices
for rental rates on trucking). Also, the support of the likelihood function
depends on model parameters, greatly complicating the study of the
asymptotic properties of maximum likelihood estimation. This poses no
particular difficulty for Bayesian methods, however.
Economic theory is used to construct the likelihood function used in
this research. Equilibrium models of strategic bidding generate a
probability density for the bids that firms submit, condition on the model
parameters (which characterized the firm's cost structures). The economic
theory of equilibrium imposes two assumptions: first, firms have correct
beliefs about the probability distribution of bids for all other firms and
second, firms maximize expected profit.
In this research, a panel data set of bidding by 21 firms for 52
contracts was constructed. Data on project specific variables that enter a
firm's cost (for instance, the distance of each firm from the project) was
also collected. For a fixed set of parameter values, the equilibrium was
computed for each bid in each project. The likelihood function is then the
product of the probability density function evaluated at each bid in each
project.
Conditional upon the observed bids and project specific cost variables,
the posterior distribution of model parameters was simulated by using a
Metropolis-Hastings algorithm. Several models were considered: a model of
competition, a model of collusive bidding, and models with unobserved,
project specific heterogeneity. Using the simulation output, it was
straightforward to compute marginalized likelihoods for each model. Bayes
factors were used to decide between the non-nested models in this research.
The preferred specification was a model of competition with unobserved,
project specific heterogeneity.
Using the posterior simulator, the econometrician's posterior beliefs
about functions of the model parameters can be explored. The posterior
distribution of firm's markups implied that the market was highly
competitive. The posterior mean was between 1 and 7 percent for most
projects. Bayes factors overwhelming favored the competitive specifications
over the collusive specifications. Prior robustness analysis was conducted
to study the sensitivity of these conclusions to the prior and in the class
of priors with the same compact support, the results were not terribly
sensitive.
A last question this research
studies was to compare alternative rules
for awarding the contract. The standard rule in bidding for government
contracts is to award the contract to the lowest responsible bidder and the
lowest bid. An alternative mechanism discussed among economists, with
highly attractive theoretical properties, is a second price auction. Here,
the firm with the lowest bid is still awarded the contract, but is paid the
amount of the second lowest bid. For each construction project, the
econometrician's posterior expectation of the cost to the government under
both rules was computed. This research found that the second price auction
results in a lower expected cost to the government, saving, on average,
between 2 and 5 percent. Readers interested in reading this research can
find it on
the author's web page. .
 Return to the top
Return to the top
GENETICS
by Siva Sivaganesan
siva@math.uc.edu
We present the annotated bibliography of the Bayesian applications in Genetics.
The list below is certainly not exhaustive, and may not even be representative.
Our intended goal here is to give the readers a sense of the current use
of Bayesian analysis in Genetics.
 J.S. SINSHEIMER, J.A. LAKE, AND R.J.A. LITTLE (1996).
Bayesian Hypothesis Testing of Four-Taxon Topologies Using Molecular
Sequence Data.
Biometrics 52, pp193-210.
J.S. SINSHEIMER, J.A. LAKE, AND R.J.A. LITTLE (1996).
Bayesian Hypothesis Testing of Four-Taxon Topologies Using Molecular
Sequence Data.
Biometrics 52, pp193-210.
Contact: Roderick J. A. Little, University of
Michigan, <rlittle@umich.edu>.
Bayesian analysis is used to test three hypotheses concerning the correct
topology from the available DNA sequences. Classical hypothesis testing is
reported to be difficult due to test the multiple alternative hypotheses
involved, while Bayesian analysis being conceptually straightforward.
Multinomial and Multivariate normal sampling models are used with uniform
priors on the parameters to obtain the posterior probabilities of the
hypotheses. Using a large simulation study to assess the frequentist
properties of the Bayesian tests, the authors conclude that Bayesian tests
are well calibrated and have reasonable discriminating power
for a wide range of realistic conditions.
 K. SJ¨OLANDER, K. KARPLUS, M. BROWN, R. HUGHEY, A. KROGH, I. S. MIAN
AND D. HAUSSLER (1996).
Dirichlet mixtures: a method for improved detection of weak but
significant protein sequence homology.
Computational Applications in Bio. Science 12, pp 327-345
K. SJ¨OLANDER, K. KARPLUS, M. BROWN, R. HUGHEY, A. KROGH, I. S. MIAN
AND D. HAUSSLER (1996).
Dirichlet mixtures: a method for improved detection of weak but
significant protein sequence homology.
Computational Applications in Bio. Science 12, pp 327-345
Contact: Kimmen Sjölander, University of California, Santa
Cruz, <kimmen@cse.ucsc.edu>.
Bayesian methods are used in finding remote homologs with lower primary
sequence identity . The authors use a Dirichlet mixture prior for amino acids
distributions. This prior is estimated using data obtained from multiple
alignment databases on observed counts of amino acids in clusters, and the
maximum likelihood method. The observed amino acid frequencies are then
used to obtain posterior estimates of amino acid probabilities at each
position in a profile.
 I. HOESCHELE, P. UIMARI, F. E. GRIGNOLA, Q. ZHANG, K.M. GAGE (1997).
Advances in Statistical Methods to Map Quantitative Trait Loci in Outbred
Populations.
Genetics 147, pp1445-1457.
I. HOESCHELE, P. UIMARI, F. E. GRIGNOLA, Q. ZHANG, K.M. GAGE (1997).
Advances in Statistical Methods to Map Quantitative Trait Loci in Outbred
Populations.
Genetics 147, pp1445-1457.
Contact : Ina Hoeschele, Virginia Polytechnic Institute
and State University, <ina@vt.edu>.
Six different statistical methods, including maximum likelihood, exact and
approximate Bayesian methods, used for gene mapping are reviewed. Authors
comment that Bayesian analysis takes full account of the uncertainty
associated with all unknowns in the problem, and allows fitting of different
models quantitative trait loci variation. References to many other related work
using Bayesian methods are also given.
 P. UIMARI AND I. HOESCHELE (1997).
Mapping-Linked Quantitative Trait Loci Using
Bayesian Analysis and
Markov Chain Monte Carlo Algorithms.
Genetics 146, pp735-743.
P. UIMARI AND I. HOESCHELE (1997).
Mapping-Linked Quantitative Trait Loci Using
Bayesian Analysis and
Markov Chain Monte Carlo Algorithms.
Genetics 146, pp735-743.
Contact: Ina Hoeschele, Virginia Polytechnic Institute
and State University, <ina@vt.edu>.
A Bayesian analysis for mapping linked quantitative trait loci(QTL) using
multiple linked genetic markers is given. This approach was motivated by the
evidence of detecting a single ``ghost QTL'' with least square analysis, when
in fact two linked QTL were segregating. Here, the authors extend existing
Bayesian linkage analysis to fit models that allow multiple linked markers;
specifically zero, one and two QTL linked to the markers. Model selection from
among these linkage models is done using data simulated under four different
designs with map positions and effects. Three different MCMC algorithms are
used to fit a mixed effect model for each data. These MCMC algorithms use
different methods of fitting, such as use of indicator variable in the model,
variable selection approach, and reversible jump MCMC. All three MCMC methods
are found to do well.
Detailed comparisons of these
methods are given. The authors conclude that it is
feasible to fit linked QTL simultaneously using
Bayesian analysis, and that it provides estimates of all genetic parameters
and can fit alternative QTL models.
 R. L. DUNBRACK, JR. AND F. E. COHEN (1997).
Bayesian statistical analysis of protein side-chain rotamer preferences.
Protein Science, 6, pp1661-1681.
R. L. DUNBRACK, JR. AND F. E. COHEN (1997).
Bayesian statistical analysis of protein side-chain rotamer preferences.
Protein Science, 6, pp1661-1681.
Contact: Roland L. Dunbrack, Jr., Institute for Cancer Research,
Philadelphia. <rl_dunbrack@fccc.edu>.
A Bayesian analysis is used to account for varying amount of information in the
Protein Data Bank for 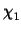 backbone dependent rotamer distributions, and to
obtain more complete estimates of these distributions. In addition, Bayesian
analysis is used to provide better estimates of the probability of occurrences
of other rare rotamers. Multinomial models and Dirichlet priors are used.
Parameters of the prior distribution are derived from previous data or from
pooling some of the present data. Model checking is done using a Bayesian
version of p-value calculated by simulating both parameter and data.
backbone dependent rotamer distributions, and to
obtain more complete estimates of these distributions. In addition, Bayesian
analysis is used to provide better estimates of the probability of occurrences
of other rare rotamers. Multinomial models and Dirichlet priors are used.
Parameters of the prior distribution are derived from previous data or from
pooling some of the present data. Model checking is done using a Bayesian
version of p-value calculated by simulating both parameter and data.
 G. PARMIGIANI, D. A. BERRY AND O. AGUILAR (1998).
Determining Carrier Probabilities for Breast Cancer Susceptibility
Genes BRCA1 and BRCA2.
American Journal of Human Genetics, 62, pp145-158.
G. PARMIGIANI, D. A. BERRY AND O. AGUILAR (1998).
Determining Carrier Probabilities for Breast Cancer Susceptibility
Genes BRCA1 and BRCA2.
American Journal of Human Genetics, 62, pp145-158.
Contact: Giovanni Parmigiani, Duke University,
< gp@stat.duke.edu.edu>.
Breast cancer susceptibility genes BRCA1 and BRCA2 have
recently been identified on the human genome. Women who carry a mutation of
one of these genes have a greatly increased chance of developing breast and
ovarian cancer, and they usually develop the disease at a much younger age,
compared with normal individuals. Women can be tested to see whether they
are carriers. A woman who undergoes genetic counseling before testing can be
told the probabilities that she is a carrier, given her family history. In
this paper we develop a model for evaluating the probabilities that a woman
is a carrier of a mutation of BRCA1 and BRCA2, on the basis of her family
history of breast and ovarian cancer in first- and second-degree relatives.
Of special importance are the relationships of the family members with
cancer, the ages at onset of the diseases, and the ages of family members
who do not have the diseases. This information can be elicited during
genetic counseling and prior to genetic testing. The carrier probabilities
are obtained from Bayes's rule, by use of family history as the evidence and
by use of the mutation prevalences as the prior distribution. In addressing
an individual's carrier probabilities, we incorporate uncertainty about some
of the key inputs of the model, such as the age-specific incidence of
diseases and the overall prevalence of mutations. There is some evidence
that other, undiscovered genes may be important in explaining familial
breast cancer. Users of the current version of the model should be aware of
this limitation. The methodology that we describe can be extended to more
than two genes, should data become available about other genes.
 G. M. PETERSEN, G. PARMIGIANI AND D. THOMAS (1998).
Missense Mutations in Disease Genes: A Bayesian Approach to
Evaluate Causality.
American Journal of Human Genetics, 62, pp1516-1524.
G. M. PETERSEN, G. PARMIGIANI AND D. THOMAS (1998).
Missense Mutations in Disease Genes: A Bayesian Approach to
Evaluate Causality.
American Journal of Human Genetics, 62, pp1516-1524.
Contact: Gloria M. Petersen, Johns Hopkins University,
< gpeterse@jhsph.edu>.
The problem of interpreting missense mutations of disease-causing genes
is an increasingly important one. Because these point mutations result in
alteration of only a single amino acid of the protein product, it is often
unclear whether this change alone is sufficient to cause disease. We propose
a Bayesian approach that utilizes genetic information on affected relatives
in families ascertained through known missense-mutation carriers. This
method is useful in evaluating known disease genes for common disease
phenotypes, such as breast cancer or colorectal cancer. The posterior
probability that a missense mutation is disease causing is conditioned on
the relationship of the relatives to the proband, the population frequency
of the mutation, and the phenocopy rate of the disease. The approach is
demonstrated in two cancer
data sets: BRCA1 R841W and APC I1307K. In both
examples, this method helps establish that these mutations are likely to be
disease causing, with Bayes factors in favor of causality of 5.09 and 66.97,
respectively, and posterior probabilities of .836 and .985. We also develop
a simple approximation for rare alleles and consider the case of unknown
penetrance and allele frequency.
 J. S. LIU AND C. E. LAWRENCE (1999).
Bayesian Inference on biopolymer models.
Bioinformatics, 15, pp38-52.
J. S. LIU AND C. E. LAWRENCE (1999).
Bayesian Inference on biopolymer models.
Bioinformatics, 15, pp38-52.
Contact: Jun S. Liu, Stanford University,
<jliu@stat.stanford.edu>.
This article introduces the Bayesian methods and its use to researchers in
bioinformatics. The article gives a tutorial introduction to Bayesian methods
using an example involving data from tossing two different coins. This example
is then further extended to illustrate application in bioinformatics using
two specific examples: sequence segmentation and global sequence alignment.
The authors state that the need for setting parameter values has been the
subject of much discussion, and that a distinct advantage of the
Bayesian method is the added modeling flexibility in the specification of
parameters. The authors comment that the rich history of computation in
bioinformatics such as dynamic programming recursions can be modified to
complete the high dimensional computation required by the Bayesian methods,
and that through the use of these recursions, the full power of the Bayesian
methodology can be brought to bear on a wide range of problems previously
addressed by dynamic programming.
 Return to the top
Return to the top
ABOUT THE SECTION
by Sudipto Banerjee
sudipto@stat.uconn.edu
We present the plans for the Section and invite students to contribute.
It is wonderful to have this new edition of the ISBA newsletter before us.
One of the sections that we plan to have in the new edition is called the
``Student's Corner''. We are hoping to include in this section abstracts of
dissertations of students who are currently doing research (like those from
ISDS, right after this note). This would not
only serve as a common platform where students can interact with one another
on common problems, but would also serve as a good indicator for the fresh
students as to what the current trends in (Bayesian) statistical research are.
Students are welcome to discuss other problems that they may have
come across in their academic or professional work.
We would also like to include plans and suggestions for common activities
such as meetings or creating web-pages where we might post discussions on
problems that we face. These problems would cover theoretical and
methodological issues as well as problems on Bayesian Data Analysis. Some of
the most widely faced problems by the modern day statistician pertains
to software related issues.
Since heavy computing is an indispensable technology
for analysing models in the Bayesian framework, many students have queries on
such issues. We feel that the student corner can serve as that much sought
after platform where students can exchange their thoughts and experiences on
such issues.
We would like to seek your
co-operation in making the ``Students' Corner'' a really useful section in
the newsletter.
We plan to have most of our
communications through e-mail. We would particularly encourage students to
send their comments on what they would like to have in this section and their
suggestions on what we can do to improve this section.
1998 Ph.D's at
ISDS, Duke University
Omar Aguilar
Latent Structure in Bayesian Multivariate Time Series Models
Advisor: Mike West
This dissertation introduces new classes of models and approaches to
multivariate time series analysis and forecasting, with a focus on various
problems in which time series structure is driven by
underlying latent processes
of key interest. The identification
of latent structure and common
features in multiple time series is first studied using wavelet based
methods and Bayesian time series decompositions of certain classes of dynamic
linear
models. The results are applied to turbulence and geochemical time
series data, the latter involving development of new time series models for
latent time-varying autoregressions with heavy-tailed components for quite
radically ill-behaved series. Natural extensions and generalizations of these
models lead to novel developments of two key model classes, dynamic factor
models for multivariate financial time series with stochastic volatility
components, and multivariate dynamic generalized linear models for non-Gaussian
longitudinal time series. These two model classes are related through
common statistical structure, and the dissertation discusses issues of Bayesian
model specification, model fitting and computation for posterior and predictive
analysis that are common to the two model classes. Two motivating applications
are discussed, one in each of the two model classes. The first concerns short
term forecasting and dynamic portfolio allocation, illustrated in a study of
the dynamic factor structure of daily spot exchange rates for a selection
of international currencies. The second application involves analyses of time
series of collections of many related binomial outcomes and arises in a project
in health care quality monitoring with the Veterans Affairs (VA) hospital
system.
Gabriel Huerta
Bayesian Analysis of Latent Structure in Time Series Models
Advisor: Mike West
The analysis and decomposition of time series is considered under
autoregressive models
with a new class of prior distributions for parameters
defining latent components. The approach induces a new class of smoothness
priors on autoregressive coefficients, provides for formal inference on
model order, including very high order models, and permits for the
incorporation of uncertainty about model order into summary inferences. The
class of prior models also allows for subsets of unit roots, and hence leads
to inference on sustained though stochastically time-varying periodicities
in time series and for formal treatment of initial values as latent
variables. As the prior modeling induces complicated forms for prior
distributions on the usual ``linear'' autoregressive parameters, exploration
of posterior distributions naturally involves in iterative stochastic
simulation with a Gibbs sampling format. Conditional posterior distributions
are available in closed form, except for those corresponding to the
parameters defining the quasi-cyclical components of the model. In this case
and to assess for the induced changes of dimensionality, a reversible jump
Markov chain Monte Carlo step is implemented. This methodology overcomes
supposed problems in spectral estimation with autoregressive models using
more traditional model fitting methods. Detailed simulation studies are presented
to evaluate the efficiency of
the sampler at detecting model
order, wavelengths and
amplitudes of cyclical components, and unitary roots
or "spikes" in the spectral density at key frequencies. Analysis,
decomposition and forecasting of several series is illustrated with
applications to EEG studies, discovering underlying periodicities in
astronomical series and climate change issues.
Additionally, an extension is
proposed for continuous autoregressive models that permits analysis of
unequally-spaced time series. This new model, that falls within the class of
dynamic linear models,
overcome some of the difficulties in both embedding
and fitting models defined through stochastic differential equation methods.
Specifically, model structure incorporates spacings through the likelihood
function and, as before, priors are specified on relevant parameters
defining latent components. Simulation from the posterior distributions is
implemented through component-wise random walk Metropolis steps with a
reversible jump. Efficiency of the method is explored as for the standard
autoregressive model with applications to irregularly sampled oxygen-isotope
records.
Colin McCulloch
High-level Image Understanding Through Bayesian Hierarchical Models
Advisor: Valen Johnson
The tasks performed by medical image analysis technicians, including
registration and segmentation, have become increasingly difficult with the
advent of three-dimensional imaging systems. To identify features in these
large images, the technician must typically engage in the tedious chore of
examining numerous lower dimensional representations of parts of the data
set, for instance slices though the volume or volume-rendered views. The
pursuit of automatic image understanding, previously sought after in
two-dimensional images for objective anatomical measurement and to reduce
operator burden, therefore has become proportionally more valuable in these
larger image datasets.
A statistical framework is proposed to automate image feature identification
and therefore facilitate the image understanding tasks of registration and
segmentation. Features are delineated using an atlas image, and a
probability distribution is defined on the locations and variations in
appearance of these features in new images from the class exemplified by the
atlas. The predictive distribution defined on feature locations in a new
image from the class essentially balances the two notions that, while each
individual feature in the new image should appear similar to its atlas
representation, contiguous groups of features should also remain faithful to
their spatial relationships in the atlas image. A joint hierarchical model
on feature locations facilitates reasonable spatial deformations from the
atlas configuration, and several local image measures are explored to
quantify feature appearance. The hierarchical structure of the joint
distribution on feature locations allows fast and robust density
maximization and straightforward Markov Chain Monte Carlo simulation. Model
hyperparameters can be estimated using training data in the form of manual
feature observations.
Given Maximum posteriori estimates an analysis is performed on in vitro
mouse brain Magnetic Resonance images to automatically segment the
hippocampus. The model is also applied to time-gated Single Photon Emission
Computed Tomography cardiac images to reduce motion artifact and increase
signal-to-noise.
Raquel Prado
Latent Structure in Non-Stationary Time Series
Advisor: Mike West
The class of time-varying autoregressions (TVAR) constitutes a suitable
class of models to describe long series that exhibit non-stationarities.
Signals experiencing changes in frequency content over time are often
appropriately modeled via relatively long AR processes with time-varying
coefficients. Using a particular DLM (dynamic linear model) representation
of TVAR models, time-domain decompositions of the series into latent
components with dynamic, correlated structures are obtained. Methodological
aspects of such decompositions and interpretability of the underlying
processes are discussed in the study of EEG
(electroencephalogram) traces.
Multiple EEG signals recorded under different ECT (electroconvulsive
therapy) conditions are analyzed using TVAR models. Decompositions of these
series and summaries of the evolution of functions of the TVAR parameters
over time, such as characteristic frequency, amplitude and modulus
trajectories of the latent, often
quasi-periodic processes, are helpful in
obtaining insights into the common structure driving the multiple series.
From the scientific viewpoint, characterizing the system structure
underlying the EEG
signals is a key factor in assessing the efficacy of ECT
treatments. Factor models that assume a time-varying AR structure on the
factors and dynamic regression models that account for time-varying
instantaneous lead/lag and amplitude structures across the multiple series
are also explored. Issues of posterior inference and implementation of these
models using Markov chain Monte Carlo (MCMC) methods are discussed.
Decompositions of the scalar components of multivariate time series are
presented. Similar to the univariate case, the state-space representation of
a VAR(p) model implies that each univariate element of a vector process
can be decomposed into a sum of latent processes where every characteristic
modulus and frequency component appears in the decomposition of each
univariate series, while the phase and amplitude of each latent component
vary in magnitude across the univariate elements. Simulated data sets and
portions of a multi-channel EEG data set are analyzed here in order to
illustrate the multivariate decomposition techniques.
Luca Tardella
Some topics in Bayesian methodology
Advisor: Michael Lavine
We extend the
methodology for robustness investigations in the framework of
nonparametric Bayesian inference.
Robustness here is intended in the sense of the determination of the
global variation of outputs given an imprecise
formulation of the inputs.
Considering nonparametric models and robustness jointly
allows an escape from the possible - inevitable -
sources of imprecision in the specification of a parametric
analysis and enhances at the same time the flexibility of the analysis.
In Bayesian inference an imprecise input is typically represented
by a class of probability measures on the unknown quantities.
In the previous literature about parametric robustness
most of the efforts have been concentrated
on classes of prior distributions for a finite collection of unknown
parameters, while the distribution of the data conditionally on those
parameters is considered to be known exactly.
Robustness with respect to misspecification
has received less attention due to the mathematical difficulties.
In the nonparametric context the two aspects are no longer separated
but they are in fact identified with the presence of a unique
unknown infinite-dimensional parameter.
We examine here nonparametric analysis within the context of
Exchangeable Tree processes
that fall in the general class of exchangeable processes
and represent a subclass of Tail-free processes.
Exchangeable Trees constitute indeed a general
class of processes and contain as particular cases
Dirichlet processes and Polya Trees, two of the most used
nonparametric priors.
We propose a predictive interpretation for an imprecise prior input
that leads us to formulate a general solution for the
global robustness investigation.
We are then able to quantify the range of linear functionals
of the conditional predictive distribution after some data have been
collected.
The larger framework implied by
enlarging the scope to an infinite-dimensional parameter
leads us to expect less robustness.
Some annoying phenomena, like dilation, are experienced,
deviating from the usual pattern in parametric robustness.
We are able to compare how this is affected by the prior inputs
and quantify how robustness can be improved by restricting
attention to particular subclasses.
Finally, a different problem is approached: simulation
from mixture distributions whose components are supported on spaces
of different dimensions. Here a novel approach is considered by
reducing the
problem to that of simulating
from a single
target
distribution that is absolutely continuous with respect to the
Lebesgue
measure on the largest support of the components.
This approach is suggested from
an alternative representation of the
simulation goal in the simplified situations when
the mixture consists only
of a one-dimensional component and a degenerate component.
Tools for suitable generalization to arbitrarily nested components
and to an arbitrary number of them are provided.
Hence two alternative methods are derived and one of them is
successfully employed in analyzing simulated data as
well as a real data set.
The new approach is designed
in order to avoid the numerical integration
needed for evaluating the relative weight of each component
and represents in the case of nested components
an alternative to the currently available
MCMC methods such as the
reversible jump algorithm (Green, 1995)
and the
composite-space approach (Carlin and Chib, 1995).
The distinguishing feature of the proposed method is the absence of
proposals for jumping between components of different dimension
or of the specification of pseudopriors.
This allows for a more automatic implementation.
Furthermore it is argued that in the actual implementation of
a Markov chain
that simulates from the absolutely continuous target distribution
one can automatically build up a chain
that allows for moving from one component to any other possible
component which possibly improves the speed of convergence.
Finally, in order to assess the mixing behaviour,
standard convergence diagnostics for
absolutely continuous stationary distributions can be used.
 Return to the top
Return to the top
BAYESIANS
IN VENEZUELA
by Bruno Sansó
www.cesma.usb.ve/~bruno
"Well, I have great respect for Bruno de Finetti and Harold Jeffreys, but
you see Luis, here we are in the 10th floor of Evans Hall over viewing
the Golden Gate. Bayesians have some work in the basement". Those were
the words of J. Neyman to Luis Raúl Pericchi in 1978. Luis finished
his Master and went to Imperial College in London to
work on a PhD under the supervision of A.C. Atkinson, working on a thesis
on Information Theory together with Bayesian and Likelihood statistics
for data transformations and model selection. Once he finished it he went
back to Caracas, Venezuela, to work at Universidad
Simón Bolívar were he started a Bayesian group.
The whole idea was motivated by the presence at USB, while Luis was
a undergraduate student in the early seventies, of
Ignacio Rodríguez Iturbe, who took a PhD in M.I.T. and went back
to his home country to work
at USB and the Instituto Venezolano de Investigaciones
Científicas; he was very interested in the possible applications
of Bayesian statistics to hydrology, in particular, in how to enlarge limited
information in some river basins, using regional information from other
sites nearby. Ignacio motivated Luis Raúl and other students to
work on Bayesian statistics and later made important contributions to its
applications to hydrology. He nowadays holds a chair in Princeton, but
he still is an influential figure in Venezuela.
The work in the basement started for Luis Raúl with a stats
lab that was called TAE, "Taller de Estadística", within the Maths
Department at USB. In the eighties TAE was a gathering place for statisticians
and several students got interested in Bayesian statistics. I remember
struggling with the 70Mb of disk space and the 8Mb of RAM memory of our
brand new Sun 3/110 workstation to squeeze in the code of Bayes 4 that
Allan Skene brought us from Nottingham and the revolutionary New S that
William Nazaret gave us from AT&T.
Few years later, in '92, several faculty members of the areas of Numerical
Analysis and Mathematical Programming, approached TAE, with the idea of
forming a more comprehensive centre. A four years grant of 800,000 dollars
from the Venezuelan Government, sponsored by the Interamerican Bank of
Development, led to the creation of CESMa
(Centro de Estadistica y Software Matematico),
under the directorship of Marianela
Lentini. The same year we organised one of Zellner's meetings on Bayesian
statistics and econometrics, which was well attended by many statisticians
from the Americas and left some people pondering the good properties of
the añejo distribution for a while.
The latest development of our
group occurred in 1996 when the USB decided
to form a new Department called "Department of Scientific Computing and
Statistics", enhancing the importance of statistics within the university.
@ Our group
The hard core of Bayesians at USB is made of the following people:
 Víctor De Oliveira (vdo@cesma.usb.ve).
Spent a year as a postdoc at the
Institute of Statistical Sciences after taking a PhD at the
University of Maryland College Park under the supervision of
Benjamin Keden. He joined us in September '98 and works in spatial problems
and geostatistics.
Víctor De Oliveira (vdo@cesma.usb.ve).
Spent a year as a postdoc at the
Institute of Statistical Sciences after taking a PhD at the
University of Maryland College Park under the supervision of
Benjamin Keden. He joined us in September '98 and works in spatial problems
and geostatistics.
 María Eglée Pérez (eglee@cesma.usb.ve).
Finished her PhD at Universidad Central de Venezuela in 1994 under the
supervision of Luis Raúl Pericchi.
She works in problems related to inference for the Exponential Family,
Bayesian analysis of discrete data and biostatistics. She has a wonderful
voice, well known among the public of the cabaret at the last Valencia.
María Eglée Pérez (eglee@cesma.usb.ve).
Finished her PhD at Universidad Central de Venezuela in 1994 under the
supervision of Luis Raúl Pericchi.
She works in problems related to inference for the Exponential Family,
Bayesian analysis of discrete data and biostatistics. She has a wonderful
voice, well known among the public of the cabaret at the last Valencia.
 José Miguel Pérez (jperez@cesma.usb.ve).
He arrived to USB in September '98, from Purdue University where he
finished a PhD under the supervision of Jim
Berger. He works in methods related to automatic priors in particular
mixture models with applications to the clustering and characterisation
of variables.
José Miguel Pérez (jperez@cesma.usb.ve).
He arrived to USB in September '98, from Purdue University where he
finished a PhD under the supervision of Jim
Berger. He works in methods related to automatic priors in particular
mixture models with applications to the clustering and characterisation
of variables.
 Luis Raúl Pericchi (pericchi@cesma.usb.ve).
Took his PhD at Imperial College in 1981. He is the most senior member
of our group and his work these days is very much focused on model comparison,
with particular interest in non subjective priors, for which he and Jim
Berger developed the Intrinsic Bayes Factor. His academic activities
span a wide range of topics including applications to medical statistics,
engineering, econometrics and official statistics. He is known as a player
of Brazilian guitar.
Luis Raúl Pericchi (pericchi@cesma.usb.ve).
Took his PhD at Imperial College in 1981. He is the most senior member
of our group and his work these days is very much focused on model comparison,
with particular interest in non subjective priors, for which he and Jim
Berger developed the Intrinsic Bayes Factor. His academic activities
span a wide range of topics including applications to medical statistics,
engineering, econometrics and official statistics. He is known as a player
of Brazilian guitar.
 Raquel Prado (raquel@cesma.usb.ve).
She is back from North Carolina since September last year; there she
took her PhD at the Institute of Statistics
and Decision Sciences under the supervision of Mike
West. She works in non stationary time series and applications of Bayesian
methods to signal processing.
Raquel Prado (raquel@cesma.usb.ve).
She is back from North Carolina since September last year; there she
took her PhD at the Institute of Statistics
and Decision Sciences under the supervision of Mike
West. She works in non stationary time series and applications of Bayesian
methods to signal processing.
 Bruno Sansó (bruno@cesma.usb.ve).
I finished my PhD at Universidad Central de Venezuela in 1992 as a
student of Pericchi working on Bayesian robustness
and spent some time at the University of Liverpool under the
supervision of Phil Brown. I now work on spatio-temporal models with
particular interest in environmental variables.
Bruno Sansó (bruno@cesma.usb.ve).
I finished my PhD at Universidad Central de Venezuela in 1992 as a
student of Pericchi working on Bayesian robustness
and spent some time at the University of Liverpool under the
supervision of Phil Brown. I now work on spatio-temporal models with
particular interest in environmental variables.
Other colleagues, with different degrees of Bayesianism share our statistical
activities, they are:
 Lelys Guenni, PhD Griffith
University, 1992. Spatio-temporal models for environmental variables,
stochastic hydrology. In her last talk she promised that it was her last
non-Bayesian one!
Lelys Guenni, PhD Griffith
University, 1992. Spatio-temporal models for environmental variables,
stochastic hydrology. In her last talk she promised that it was her last
non-Bayesian one!
 Raúl Jiménez,
PhD Universidad Central de Venezuela, 1992. Asymptotic behaviour of stochastic
processes, theory of statistical information.
Raúl Jiménez,
PhD Universidad Central de Venezuela, 1992. Asymptotic behaviour of stochastic
processes, theory of statistical information.
 Isabel Llatas, PhD Wisconsin-Madison,
1987. Experimental design, multivariate statistics, statistical quality
assessment. She is currently the director of CESMa.
Isabel Llatas, PhD Wisconsin-Madison,
1987. Experimental design, multivariate statistics, statistical quality
assessment. She is currently the director of CESMa.
 José Luis Palacios, PhD
Berkeley 1982. Random walks on graphs, discrete stochastic processes, combinatorics.
José Luis Palacios, PhD
Berkeley 1982. Random walks on graphs, discrete stochastic processes, combinatorics.
 Adolfo Quiroz, PhD MIT 1986. Nonparametric
methods, goodness of fit for multivariate data.
Adolfo Quiroz, PhD MIT 1986. Nonparametric
methods, goodness of fit for multivariate data.
 Leonardo Saab, Master Wisconsin
Madison, 1985. Statistical applications of quality management, growth curves
for Venezuelan children.
Leonardo Saab, Master Wisconsin
Madison, 1985. Statistical applications of quality management, growth curves
for Venezuelan children.
@ Working environment
USB has a very pleasant campus in the
outskirts of Caracas, the capital of Venezuela. The weather is fairly mild
thanks to the 1,000 plus meters above the sea level and the low density
of the urban development around the campus. Tropical gardens, that are
part of the university's pride, surround the buildings and create a very
pleasant compare our campus to a resort!
At CESMa we work mainly with Sun workstations, at last count they were
around 16, the last arrival being a powerful 450 Enterprise with two processors.
We have the tradition of naming them after characters of the Latin American
literature and, as a result, we have a colourful network populated with
thieves, whores, heroes, fantastic people created by the imagination of
García Márquez, Vargas Llosa and the like.
We have around 20 students following courses in three programmes:
Diploma Master and PhD. All three programmes are quite new: they have been
in place for less than two years, nevertheless they already seem to be
a success.
We have definitely climbed some steps up from the basement during the
last years and in spite of the uncertainties that we live these days in
our country, I think that the future is bright for Bayesian statistics
in Venezuela.
This article is available in html with links and pictures at
www.cesma.usb.ve/novedades/isbae.html
.
 Return to the top
Return to the top
NEWS FROM THE WORLD
by Antonio Pievatolo
marco@iami.mi.cnr.it
* denotes an ISBA activity
@ Events
International Workshop on Objective Bayesian Methodology.
June 11-13, 1999. Valencia, Spain.
The workshop is sponsored by the Universitat de València
for its 500th anniversary. The programme features
17 invited lectures (with discussion) on the following topics:
objective priors and frequentist statistics,
determination of objective priors in
important problems, priors for objective Bayesian testing and model
selection, objective priors in nonparametric analysis,
the roles of objective Bayesian analysis. The submission of
contributed papers for two plenary poster session is
encouraged (deadline April,30).
INFO: http://www.uv.es/~bernardo/workshop.html
Workshop on Bayesian Nonparametric Statistics. July
23-28, 1999. Reading University, UK.
The Workshop is being organised by the Research Section of the
Royal Statistic Society and funded by the Engineering and Physical
Sciences Reseach Council (EPSRC).
Well-known researchers and leaders in the field have been invited
to speak on methods, theory and applications.
INFO: http://www.stats.bris.ac.uk/~guy/Research/Workshop.html
MaxEnt '99. August
2-6, 1999. Boise State University, Boise, Idaho.
MaxEnt '99 is the Nineteenth International Conference on
Maximum Entropy and Bayesian Methods. There is no explicit
deadline for sending an abstract.
INFO: http://www.maxent99.boisestate.edu/
1999 NBER/NSF Time Series Conference. August
23-25, 1999. Academia Sinica, Taipei, Taiwan.
The deadline for the submission of an abstract is June 1, 1999.
INFO: http://www.sinica.edu.tw/econ/nber-nsf/
Case Studies in Bayesian
Statistics, Workshop 5. September
24-25, 1999. Carnegie Mellon University, Pittsburgh, Pennsylvania.
The Workshop aims to explore the interplay between statistical theory and
practice in the context of concrete and collaborative research projects.
INFO: http://lib.stat.cmu.edu/
bayesworkshop/Bayes99.html
@ Internet Resources
* The ISBA Web Page. We remind you of the ISBA
Web Page. It gives information on the ISBA activities, as well as
links to Bayesian resources.
URL: http://www.bayesian.org/
* Bayesian Abstract Archive. A searchable interactive
archive of abstracts of papers, books, theses, and conference
presentations is available at the Institute of Statistics and
Decision Sciences at Duke University. The Archive is sponsored by
ISBA and SBSS.
The Editor of the Archive
encourages you to submit your abstracts, so that it becomes
a valuable resource to all Bayesians.
URL: http://www.isds.duke.
edu/isba-sbss/
Bayesian Model Averaging. You can browse this document at the
web site of AT&T Research. It contains downloadable S-PLUS
code that implements BMA for various classes of widely used
regression models, a list of
papers on BMA and a list of
people interested in BMA.
URL: http://www.research.att.com/~volinsky/bma.html
@ Research Opportunities
Fifth Framework Programme.
The Fifth Framework Programme (FP5) sets out the priorities
for the European Union's research, technological
development and demonstration activities (RTD) for the
period 1998-2002, with an agreed budget of 13,700 million Euro.
Four focussed Thematic programmes and three
wide ranging Horizontal programmes have been defined.
The Thematic Programmes have the following names:
``Quality of life and management of living resources'',
``User-friendly information society'', ``Competitive and
sustainable growth'', and ``Energy, environment and sustainable
development''.
Calls for proposals for RTD will be issued within each
Programme. The first call has been launched last March.
FP5 is open to all legal entities established in the
Member States of the EU and in any of the other States associated
to the Programme. Participation to ``third countries''
is governed by common conditions which are applied throughout
FP5.
FP5's homepage is http://www.cordis.lu/fp5/home.html.
Some documents are available
for download in MS Word 6 or PDF.
@ Awards and Prizes
* Third Mitchell Prize.
The Mitchell Prize is named for Toby J. Mitchell,
who made incisive contributions to statistics, especially
in biometry and engineering applications.
The Prize will be announced and presented at the August 1999
Joint Statistical Meetings in Baltimore and will be awarded
in recognition of an outstanding
paper describing how a Bayesian analysis has solved an important
applied problem.
Beginning this year, the Prize will be awarded annually
under the cosponsorship of the ASA Section on Bayesian Statistical
Science (SBSS), the ISBA,
and the Mitchell Prize Founders' Committee.
To be eligible for the 1999 Prize, a paper will either have appeared in
a refereed journal or refereed conference proceedings since January 1 1997,
or be scheduled for future publication in a refereed outlet. Submissions
should be received by May 15, 1999.
INFO: http://www.stat.duke.edu/sites/mitchell.html
@ Miscellanea
First Mexico Workshop on Bayesian Statistics. September
9-12, 1998. IIMAS-UNAM, Mexico City, Mexico. This workshop, the first
of its kind in Mexico, was held at the Universidad Nacional Autónoma
de México (UNAM) and was organised by the Mexican Statistical
Association (AME), two Institutes of the UNAM
(IIMAS and IMATE), and the Autonomous Technological Institute of
Mexico (ITAM). The programme consisted of three short courses
(Decision Theory, Bayesian Inference, and Computational Methods) and
two research sessions, one of which was devoted to applications.
DEBUG. In September 1998 a German BUGS user group
(DEBUG - Deutsche BUGS-User-Gruppe)
was founded. The group has the following aims:
to provide a forum for exchange of experiences with the program BUGS;
to promote exchange of examples;
to bundle the interests of the users when repair and further development
are discussed; to provide guidance through the literature.
INFO: http://userpage.ukbf.
fu-berlin.de/~debug/
Workshops on Risk at RSS99. July 12-15, 1999. University
of Warwick, Coventry, UK. The deadline for submission of contributed
papers at the International Conference of the Royal Statistical
Society has passed, however contributions to the scheduled
specialized workshop are welcome. Two of these workshops are
related to Risk Assesment.
INFO: http://www.warwick.ac.uk/statsdept/rss99/workshop.html
 Return to the top
Return to the top
JOINING THE ISBA
The form can be found either at the
ISBA web site or
here as postscript file.
There are many benefits associated with joining the society not the least of
which is the subscription to the ISBA Quarterly Newsletter. Please complete
this form and return it with your membership fee to:
Professor Valen Johnson, ISBA Treasurer
Institute of Statistics & Decision Sciences
223 Old Chem Building
Box 90251
Duke University
Durham, NC USA 27708-0251
voice:(919)-684-8753
fax: (919)-684-8594
valen@stat.duke.edu
http://www.isds.duke.edu/~valen/
I wish to become a member of ISBA
I wish to renew my ISBA membership
Name
Institution/Company
Department
Street Address
City, State/Province
Country, ZIP/Postal Code
Phone Fax
E-mail
I want the information available for others: Yes
No
Membership fee (*) for 1999 is U.S. $25.00.
 Enclose check in U.S. $ payable to International Society for
Bayesian Analysis
Enclose check in U.S. $ payable to International Society for
Bayesian Analysis
 Credit card payment
Credit card payment
AmeExpress  MasterCard
MasterCard  VISA
VISA
Card # Exp.
Date, Signature
(*) The membership fee for calendar year, Jan. 1 to Dec. 31, 1999 is U.S.
$25.00. ISBA also has reduced rates for certain individuals. This reduced
rate has been fixed at $10 for 1999. People who can apply for that include
students (full proof of status; maximum of 4 years in a row) and permanent
residents of selected countries. A country qualifies for the reduced rate in
1999 if its GNP per capita based on the World Bank Data for 1996 is no
greater than $6,000. For example, this includes the countries where our
three current Chapters reside (Chile, India and South Africa).
 Return to the top
Return to the top
ISBA OFFICERS
Executive Committee
President: John Geweke
Past-President: Susie Bayarri
President-Elect: Philip Dawid
Treasurer: Valen Johnson
Executive Secretary: Michael Evans
Board Members
Mark Berliner, Enrique de Alba, Petros Dellaportas, Alan Gelfand,
Ed George, Jayanta Ghosh, Malay Ghosh, Jay Kadane, Rob Kass,
Daniel Peña, Luis Pericchi, Sylvia Richardson
EDITORIAL BOARD
Editor
Fabrizio Ruggeri <fabrizio@iami.mi.cnr.it>
Associate Editors
Bayesian Teaching
Jim Albert <albert@math.bgsu.edu>
Students' Corner
Sudipto Banerjee <sudipto@stat.uconn.edu>
Applications
Sujit Ghosh <sghosh@stat.ncsu.edu>
Software Review
Gabriel Huerta <gabriel@bayes.stats.nwu.edu>
News from the World
Antonio Pievatolo <marco@iami.mi.cnr.it>
Interviews
David Rios Insua <d.rios@escet.urjc.es>
Michael Wiper <mwiper@est-econ.uc3m.es>
Annotated Bibliography
Siva Sivaganesan <siva@math.uc.edu>
Bayesian History
Isabella Verdinelli <isabella@stat.cmu.edu>
Corresponding Editors
Carmen Armero <carmen.armero@uv.es>
Marilena Barbieri <marilena@pow2.sta.uniroma1.it>
Christopher Carter <imchrisc@ust.hk>
Roger M. Cooke <r.m.cooke@twi.tudelft.nl>
Petros Dellaportas <petros@aueb.gr>
Eduardo Gutierrez Peña <eduardo@sigma.iimas.unam.mx>
Robert Kohn <robertk@agsm.unsw.edu.au>
Jack C. Lee <jclee@stat.nctu.edu.tw>
Leo Knorr-Held <leo@stat.uni-muenchen.de>
Udi Makov <makov@rstat.haifa.ac.il>
Marek Meczarski <mecz@sgh.waw.pl>
Renate Meyer <meyer@stat.auckland.ac.nz>
Suleyman Ozekici <ozekici@boun.edu.tr>
Wolfgang Polasek <wolfgang@iso.iso.unibas.ch>
Raquel Prado <raquel@cesma.usb.ve>
Josemar Rodrigues <josemar@icmc.sc.usp.br>
Alfredo Russo <arusso@unq.edu.ar>
Antonia Amaral Turkman <antonia.turkman@cc.fc.ul.pt>
Brani Vidakovic <brani@stat.duke.edu>
Hajime Wago <wago@ism.ac.jp>
Simon Wilson <swilson@stats.tcd.ie>
Lara Wolfson <ljwolfson@byu.edu>
Karen Young <mas1ky@ee.surrey.ac.uk>
Mailing address: ISBA NEWSLETTER - CNR IAMI - Via Ampère 56 -
20131 Milano (Italy)
E-mail: isba@iami.mi.cnr.it
Phone: +39
0270643206 Fax: +39 0270643212
 Return to the top
Return to the top