Second Workshop on

BAYESIAN INFERENCE IN STOCHASTIC PROCESSES

Villa Monastero, Varenna (LC), Italy

31 May - 2 June, 2001

TALKS


Maria Concepcion Ausin

Bayesian inference and prediction in M/G/1 queues using a phase type approximation

Any continuous probability distribution on the positive real line may be obtained as the uniform limit of a sequence of finite mixtures of Erlang distributions. This general result allows us to approximate the general service time distribution in a M/G/1 queue using a mixture of such distributions. A Bayesian procedure based on reversible jump Markov Chain Monte Carlo methods can be used in order to make inference on the parameters of the mixture with an unknown number of components. Mixtures of Erlang distributions belong to the set of probability distributions of phase type. A phase type distribution is the distribution of the time until absorption in a finite Markov chain with one absorbing state. If the service time distribution in a stable M/G/1 queue is of phase type, it is possible to consider some measures of the system as first passage times in appropriate infinite state Markov chains. Then, an explicit evaluation of measures such as the stationary queue size, waiting time and busy period distributions can be obtained. Given the interarrival and service data, the predictive distributions of these quantities are obtained using the MCMC output. We illustrate this approach with various practical examples.

David Conesa and Carmen Armero

Bayesian inference and prediction in groups of bulk service queues

When analyzing different applications of bulk service queues (systems in which the service facility has the capability to serve various customers simultaneously),the usual general scenario consists of various stable queues with the same characteristics operating independently. In this work we review how to study the congestion of these kind of systems in the steady-state. In particular, our first step is to make inference on the parameters (arrival and services rates of each queue) governing the whole system. To do so, we perform a hierarchical Bayesian analysis in which we specify the prior distribution in two stages. In the first one (and taking into account that all the queues have the same characteristics), we assume that the parameters of each queue are a random sample from a common distribution with some unknown hyperparameters, and, in the second one, we select a hyperprior distribution for those unknown hyperparameters. The data required to update this prior information is collected by observing the arrival and service processes of each queue individually, recording for each one, a fixed number of consecutive interarrival times and service times. As usual in Queueing Theory, once it is assumed that all the queues are working in equilibrium, their congestion is better described through the so-called measures of performance (number of customers, waiting times, idle and busy periods, ...), so our next focus is how to compute the posterior predictive distribution of these variables. In this point, we consider two possibilities. The first one, is devoted to analyze the congestion in each one of the queues considered in the experiment, while the second one deals with the congestion of a generic queue with the same characteristics that is not included in the experiment. In both cases, all these predictives are computed by using numerical procedures to simulate from posterior distributions (such as MCMC) and numerical inversion of transforms.

A. Philip Dawid

Inference for Stochastic Processes - Some Bayesian and Prequential Considerations

Many aspects of classical parametric statistical inference, for example the definition of efficiency, or asymptotic normality of the sampling distribution of the maximum likelihood estimator, were originally formulated for problems with independent and identically distributed observations, and do not readily generalise to the case of stochastic process models. By contrast, Bayesian parametric inference for stochastic processes remains just as straightforward as in the IID case. Similarly, when it comes to assessing the validity of a model, the general methods of Prequential Analysis continue to apply, again without any adjustment, to stochastic process models. In both cases, the results obtained are simple and appealing. I shall discuss how the form of such Bayesian and prequential inferences can serve as a valuable guide to formulating appropriate frequentist definitions and theorems.

Reference

Dawid, A. P. (1991). Fisherian inference in likelihood and prequential frames of reference (with Discussion). JRSS(B) 53, 79 - 109.

Michele Di Pietro

Inference for Discretely Sampled Diffusions under Jeffreys' Prior

Likelihood-based inference about the parameters of a diffusion is rarely straightforward. The transition density, and hence the likelihood, can only be recovered by solving the stochastic differential equation associated with the diffusion. This difficulty carries over to Bayesian approaches, and to the derivation of Jeffreys' prior. The only Bayesian approaches existing today rely on a normal approximation to the transition density, the Euler discretization scheme. We show that this method is effective in approximating the likelihood, but not Jeffreys' prior. As an alternative, we consider a closed-form sequence of functions that approximates the transition density, proposed by Ait-Sahalia (1990, 2000) in a frequentist setting, and based on a Hermite-polynomial expansion. We show how to modify this sequence so it can be used in a Bayesian framework. The resulting tool provides good approximations to both the likelihood and Jeffreys' prior. We illustrate the accuracy of the methodology using a financial example.

Petar M. Djuric and Jianqiu Zhang

Equalization and symbol estimation in wireless communications by particle filtering

In wireless communications two critical operations are channel equalization and symbol estimation. The received signals contain noise and are distorted by the communication channel, which may be time and/or frequency selective and/or time-varying. The ultimate objective of the receiver is estimation of the transmitted symbols with high accuracy. The high accuracy, however, can only be achieved if the symbol estimation is preceded by accurate channel equalization. The two operations are closely intertwined, especially in the case of blind channel equalization. In the literature, much of the reported work on channel equalization and symbol estimation has been on methods that are based on the maximum likelihood principle. In addition, most of the assumptions are simplistic and include linear models and Gaussian distributed noise. In this paper we relax some of these assumptions and apply particle filters. The underlying philosophy used in the design of such filters is the representation of the posterior distribution of state variables (the unknowns of the system) by a set of particles. Each particle is given an importance weight so that the set of particles and their weights represents a random measure that approximates the desired posterior distribution. As new information becomes available, these particles propagate recursively through their state space, and their weights are modified using the principles of Bayesian theory. In the paper we develop a procedure for equalization and symbol estimation based on particle filtering and compare it with some standard methods.

Ilenia Epifani, Sandra Fortini and Lucia Ladelli

A Characterization for Mixtures of Minimal Continuous Time Markov Chains

Recently, Fortini, Ladelli, Petris and Regazzini (1999), have characterized the law of a chain which is mixture of Markov laws through the condition of partial exchangeability of successor states that the chain generates. An analogous characterization is obtained for the law of a minimal continuous time jump process. More precisely, we have proved that the distribution of a continuous time minimal chain is a mixture of Markov laws if and only if the jump process generates a partially exchangeable array of successor states and holding times and a symmetry condition on the law of the holding times holds. If the last symmetry condition is removed, that is the process meets only the condition of partially exchangeability, we resort to mixtures of Semi-Markov laws.

Marco Ferreira, Mike West, David Higdon and Herbie Lee

Bayesian Inference in a New Class of Multi-Scale Time Series Models

We introduce a class of multi-scale models for time series. The novel framework couples 'simple' standard Markov models for the time series stochastic process at different levels of aggregation, and links them via 'error' models to induced a new and rich class of structured linear models reconciling modelling and information at different levels of resolution. Jeffrey's rule of conditioning is used to revise the implied distributions and ensure that the probability distributions at different levels are strictly compatible. Our construction has several interesting characteristics: a variety of autocorrelation functions resulting from just a few parameters, the ability to combine information from different scales, and the capacity to emulate long memory processes. There are at least three uses for our multi-scale framework: to integrate the information from data observed at different scales; to induce a particular process when the data is observed only at the finest scale; as a prior for an underlying multi-scale process. Bayesian estimation based in MCMC analysis is developed, and issues of forecasting are discussed. Two interesting applications are presented: in the first application, we illustrate some basic concepts of our multiscale class of models through the analysis of the flow of a river. In the second application we use our multiscale framework to model daily and monthly log-volatilities of exchange rates.

Alan Gelfand

Bayesian Inference for Multivariate Spatial Processes

By now, Bayesian inference for univariate spatial processes is fairly well established though various challenging modeling and computational issues remain. I will discuss these briefly in the process of introducing basic ideas. However, the main focus of this talk will be Bayesian inference for point-referenced random vectors. Here the foregoing challenges are exacerbated. I will attempt to elaborate these matters, in the process providing a variety of illustrations.

Daniela Golinelli

Bayesian inference in hidden stochastic population processes

The idea of using stochastic modeling versus deterministic modeling for studying complex biological, ecological, physical and epidemiological processes has recently received considerable attention. Even though a lot is known about the mathematical properties of continuous time stochastic population processes, it is rare to see these models fit to data. They tend to be impractical since it is seldom possible to observe the process completely due to experimental constraints. In the presence of incomplete data, the computation of the likelihood function requires a difficult integration step over a complex space. Advances in stochastic integration methods, like Markov chain Monte Carlo (MCMC) and reversible jump Markov chain Monte Carlo (RJMCMC), have led to the development of inferential methods that would not have been feasible a few years ago. In this work, I consider parameter estimation in hidden continuous time stochastic population processes. In particular, I focus my attention on two classes of hidden population processes: hidden linear birth-death processes and hidden two-compartment processes. The consideration of the last class of models is motivated by research concerning the process of blood cell production. I present algorithms for Bayesian inference in these models under various observational schemes such as partial information at event times and hidden event times with discrete observations. The algorithms proposed in this work are quite general, and therefore it should be possible to extend them to more complicated hidden stochastic population models. Also, such an approach could be helpful to design better experiments for analyzing hidden population processes. The idea is to use such methodology to understand how often and what type of observations are needed in order to make effective inference about the event intensities of the hidden population processes.

Gabriel Huerta, Bruno Sansò and Jonathan R. Stroud

Space-time analysis of Mexico City ozone levels

We consider hourly readings of ozone concentrations over Mexico City and propose a model for spatial as well as temporal interpolation and prediction. The model is based on regressing the observed readings on a set of meteorological variables, such as temperature and humidity. A few harmonic components are a dded to account for the main periodicities that ozone presents during a given day. The model inco rporates spatial covariance structure for the observations and the parameters that define the harm onic components. Using the Dynamic Linear model framework, we show how to compute predictive valu es and smoothed means of the ozone spatial field.

Aparna V. Huzurbazar

Bayesian Analysis for Semi-Markov Models

When a continuous time semi-Markov process defines transition times between a finite number of states and interest focuses on estimating densities, survivals, hazards, or predictive distributions, flowgraph models provide a way of presenting the model and an associated methods for data analysis. I will introduce flowgraph models and related saddlepoint methods for problems in systems engineering and reliability. An important advantage of flowgraph / saddlepoint methods is the ability to construct likelihoods for incomplete data. Applications to a cellular telephone network are given and advantages over direct simulation are presented.

Joseph B. Kadane and George G. Woodworth

Hierarchical Models for Employment Decisions

In the United States Federal law prohibits discrimination in employment decisions against persons in certain protected categories. The common method for measuring discrimination involves a comparison of some aggregate statistic for protected and non-protected individuals. This approach is open to question when employment decisions are made over an extended time period. We use hierarchical proportional hazards models with a smooth, time varying log odds ratio to analyze the decision process. We use a smoothness prior (linear trend plus integrated Wiener process with precision tau) for the log odds ratio. The analysis is somewhat sensitive to the smoothness parameter and we use the Bayes factor to select an appropriate value.

Examples of two litigated cases will be presented.

Lynn Kuo and Tae Yang

Bayesian Binary Segmentation Procedure for a Poisson Process with Multiple Changepoints

We observe n events occurring in (0,T] taken from a Poisson process. The intensity function of the process is assumed to be a step function with multiple changepoints. We propose a Bayesian binary segmentation procedure for locating the changepoints and the associated heights of the intensity function. We conduct a sequence of nested hypothesis tests using the Bayes factor or the BIC approximation to the Bayes factor. At each comparison in the binary segmentation steps, we only need to compare a single-changepoint model to a no-changepoint model. Therefore, this method circumvents the computational complexity we would normally face in problems with an unknown (large) number of dimensions.
A simulation study and an analysis on a real data set are given to illustrate our methods.

Herbert Lee, David Higdon, Marco Ferreira and Mike West

MCMC Methods for Inverse Problems on a Grid

A variety of applied problems involve inference for a spatially-distributed parameter, where inference is done on a grid, either because of the physical problem (e.g., the natural pixels in image analysis), or for modelling convenience (e.g., soil permeabilities which vary spatially). The problem is then one of modelling a high-dimensional parameter, which grows difficult as the grid becomes large. The process may be even more difficult when the likelihood involves complex computer code. We discuss several methods for approaching this problem in the Bayesian context. We illustrate these methods on a hydrology example, where the estimation of soil permeabilities and our uncertainty about these estimates is crucial for engineers involved in contaminant clean-up or oil production, yet the problem is extremely difficult because of sparse data and a likelihood which depends on the solutions of differential equations.

Antonio Lijoi, Pier Luigi Conti and Fabrizio Ruggeri

A Bayesian approach to the analysis of telecommunications system performance

Fractional Brownian Motion (FBM) is used to model cumulative traffic network. According to the value assumed by the self-similarity parameter H, FBM is an independent increment process or, alternatively, a process featuring long-range dependence. In a Bayesian setting, we consider the problem of estimating H and the ``loss probability''. The latter coincides with the probability of losing traffic data and represents a measure of the quality of the service provided by the system. Finally, we aim at giving some empirical evidence of the relationship between performance of the system and presence of long-range dependence with an application to a real dataset.

Brunero Liseo, Maria Maddalena Barbieri and Donatella Mandolini

Bayesian analysis for estimating incidence of HIV infection

The problem of estimating the usually unknown time since infection for individuals positive to an HIV (human immunodeficiency virus) test is considered. For each individual two random quantities are defined: the time T from the moment of infection to the first positive test, and the level of CD4 cells in the blood at the time of discovery. A model proposed by Berman (1990) is adopted to describe the change of CD4 level with time since infection. Gaussian process theory is used to derive the posterior distribution of T conditionally on the level of CD4 cells. The information in the data set is used to estimate the moments of the prior distribution of time since infection. This empirical Bayes approach is investigated here from a robust Bayesian viewpoint, on the basis of an Italian cohort of seroconverted individuals from a multicenter study.

Key words: CD4 cells number, HIV infection, robust Bayesian analysis, stationary Gaussian process, time of infection.

1. Introduction

It is essential to understand and to be able to predict the progression of HIV infection to control the epidemic of acquired immunodeficiency sindrome (AIDS). However, for most of the individuals positive to an HIV test the date of infection is unknown. HIV infection is accompanied by a gradual deterioration of the immune system and abnormal measurements of immunological variables are observed. In particular one of the most used biological ``marker'' to infer about the otherwise unknown time of infection is the CD4-lymphochyte (CD4) cells counts per mm3 of blood. This variable shows high variability among non infected individuals and a downward relation with time since infection (see for example Lange, Carlin and Gelfand (1992) and references therein).

Berman (1990) used a mixed inferential approach to produce a predictive device in order to estimate the elapsed time since infection for a single individual on the basis of his/her CD4 counts. His idea is to use repeated measures on a cohort of seroconverted individuals to infer about the prior distribution of T, defined as the (known) time of first positive test minus the (unknown) time of initial infection .

In this paper we discuss the Berman's approach from a robust Bayesian viewpoint by considering the class of all prior distributions compatible with the information provided by the data set. Our aim is to show to what extent time predictions based on the Gaussian model can be sensitive to the prior distribution. We use an Italian cohort of seroconverted individuals from a multicenter study to show that Berman's estimates are robust enough for regular values of CD4 count, whereas estimates show a strong sensitivity to the prior distribution for extreme values of CD4 cells number.

2. The Berman's model

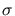Berman (1990) and Dubin et al. (1994) modelled the CD4 count in a HIV negative individual, as: X(t) = exp{Z(t)}, where Z(t) is a Gaussian stationary process with mean parameter $ \mu$ and standard deviation $ \sigma$. It is also assumed that the process X(t) is modified at the moment of infection by a dumping factor. Then, if t0 is the time of infection, the stochastic process describing the CD4 evolution is given by

X(t)e- $\scriptstyle \delta$(t - t0),   t > t0,

where $ \delta$ > 0 is the decay rate parameter.

The ultimate objective of the model is to estimate the distribution of the elapsed time since infection T for the individuals who are found, for the first time, HIV positive. The essentially simplifying assumption that T is independent from the process X(t) is made.

Let t0 be the unknown time of infection for a given individual and let t1 be the time elapsed between the first and the second CD4 measurement. If the first HIV positive test occurs Ttime units after infection, the CD4 counts at the two visits are X(t0 + T)e- $\scriptstyle \delta$T and X(t0 + t1 + T)e- $\scriptstyle \delta$(T + t1), respectively.

Since the process X(t) is stationary, the distribution of the above random variables does not depend on t0 and t0 = 0 can be assumed. Denoting R(t) = Z(t) - $ \delta$t, focus will be on the random variables: R(0), the log of CD4 count at the moment of infection; R(T), the log of CD4 count at the time of first positive test; R(T + t1), the log of CD4 count at the second visit .

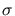The unknown quantities are $ \mu$, $ \sigma$ and $ \delta$. The first two parameters are easily estimable since they represent the mean and the standard deviation of the CD4 counts in the non infected population. To estimate $ \delta$ Berman (1990) suggests to use the sample average of the log counts decay rates, namely:

 
$\displaystyle \hat{\delta}$ = $\displaystyle {\frac{1}{n}}$$\displaystyle \sum_{j=1}^{n}$$\displaystyle {\frac{r^1_j-r^2_j}{t_{1j}}}$. (1)

where r1j and r2j are the CD4 measured at the first and second visit, with a lag time t1j, for each individual j ( j = 1,..., n).

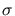
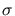It can be shown (Berman, 1990) that $ \left(\vphantom{ [R(t)-\mu]/\sigma\left\vert \delta T/\sigma=t \right) }\right.$[R(t) - $ \mu$]/$ \sigma$$ \left\vert\vphantom{ \delta T/\sigma=t }\right.$$ \delta$T/$ \sigma$ = t$ \left.\vphantom{ \delta T/\sigma=t }\right)$ $ \left.\vphantom{ [R(t)-\mu]/\sigma\left\vert \delta T/\sigma=t \right) }\right.$ $ \sim$ N(- t, 1).

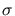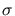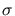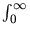
If $ \pi$(t) denotes the prior distribution of the transformed quantity $ \delta$T/$ \sigma$, then the posterior distribution of $ \delta$T/$ \sigma$conditionally on (R(t) - $ \mu$)/$ \sigma$ = x is given by $ \pi$(t)$ \phi$(x + t)/$ \int_{0}^{\infty}$$ \pi$(y)$ \phi$(x + y)dy, where $ \phi$( . ) denotes the standard normal density function.

Berman also shows how to use sample information to estimate the prior moments of $ \pi$(t). His elegant derivation is based on Hermite polynomials and stems from the fact that, for every m = 0, 1, 2,...: I   E$ \left\{\vphantom{H_m(\frac{R-\mu}{\sigma})}\right.$Hm($ {\frac{R-\mu}{\sigma}}$)$ \left.\vphantom{H_m(\frac{R-\mu}{\sigma})}\right\}$ = (- 1)mI   E$ \left\{\vphantom{(\frac{\delta T}{\sigma})^m }\right.$($ {\frac{\delta T}{\sigma}}$)m$ \left.\vphantom{(\frac{\delta T}{\sigma})^m }\right\}$, where Hm denotes the Hermite polynomial of degree m. Then the estimated moments are associated to a given form of the prior distribution to produce posterior estimates of T, for a given level of x.

3. Robust Bayesian analysis

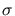One possible improvement of the Berman's approach is to eliminate the indeterminacy of the choice of the prior density of $ \delta$T/$ \sigma$ using a robust Bayesian approach (Berger, 1994), i.e. by considering the class of all prior distributions compatible with the sample estimates of the prior moments.

The normality assumption for the stochastic process together with the Hermite polynomial theory allows to produce estimates for the first m moments of the prior, say $ \mu_{1}^{}$,$ \mu_{2}^{}$,...,$ \mu_{m}^{}$. 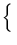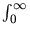This information will be then used to define $ \Gamma_{m}^{}$, the class of all prior distributions with the first m moments given (Goutis, 1994; Dall'Aglio, 1995), namely $ \Gamma_{m}^{}$ = $ \left\{\vphantom{ \pi: \int_0^{\infty} y^k \pi(dy)=\mu_k; k=1,\ldots,m }\right.$$ \pi$ : $ \int_{0}^{\infty}$yk$ \pi$(dy) = $ \mu_{k}^{}$;k = 1,..., m$ \left.\vphantom{ \pi: \int_0^{\infty} y^k \pi(dy)=\mu_k; k=1,\ldots,m }\right\}$.

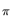
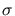
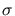Let $ \rho$($ \pi$, x) = I   E$\scriptstyle \pi$$ \left(\vphantom{ \delta T/\sigma \left\vert [R(t)-\mu]/\sigma=x \right) }\right.$$ \delta$T/$ \sigma$$ \left\vert\vphantom{ [R(t)-\mu]/\sigma=x }\right.$[R(t) - $ \mu$]/$ \sigma$ = x$ \left.\vphantom{ [R(t)-\mu]/\sigma=x }\right)$ $ \left.\vphantom{ \delta T/\sigma \left\vert [R(t)-\mu]/\sigma=x \right) }\right.$be the posterior expectation of the elapsed time since infection for an individual with a rescaled count x at his first positive visit. 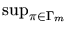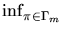We will use an algorithm based on semi-infinite linear programming proposed by Dall'Aglio (1995) to compute $ \overline{\rho}$(x) = $ \sup_{\pi \in \Gamma_m}^{}$$ \rho$($ \pi$, x)and $ \underline{\rho}$(x) = $ \inf_{\pi \in \Gamma_m}^{}$$ \rho$($ \pi$, x). The distance between $ \overline{\rho}$(x) and $ \underline{\rho}$(x) at a given level of x should be interpreted as a measure of accuracy of the prediction.


References

  • Berger, J.O. (1994). An overview of robust Bayesian analysis (with discussion), Test, 3, 5-125.

  • Berman, S. (1990). A stochastic model for the distribution of HIV latency time based on T4 counts, Biometrika, 77, 733-741.

  • Dall'Aglio, M. (1995). Problema dei momenti e programmazione lineare semi-infinita nella robustezza bayesiana. Ph.D. Thesis, Dip. di Statistica Prob. e Stat. Appl., Università di Roma ``La Sapienza" (in Italian).

  • Dubin, N., Berman, S., Marmor, M. Tindall, B. Jarlais, D.D., Kim, M. (1994). Estimation of time since infection using longitudinal disease marker data, Statistics in Medicine, 13, 231-244.

  • Goutis, C. (1994). Ranges of Posterior Measures for Some Classes of Priors with Specified Moments, International Statistical Review, 62, 245-256.

  • Lange, N., Carlin, B.P. and Gelfand, A.E. (1992). Hierarchical Bayes models for the progression of HIV infection using longitudinal CD4 T-cell number, J. of Amer. Stat. Assoc., 87, 615-632.

Juan Miguel Marin, Lluis Pla and David Rios Insua

Some forecasting models for sow farm management

Sow management requires forecasting models for the farm population structure, with sows potentially belonging to up to thirty six stages. We describe several models for such purpose based on Markov chains and Dynamic Linear Models.

Peter Mueller

ANOVA on random functions

We consider inference for related random functions indexed by categorical covariates X=(X1, ..., Xp). The functions could, for example, be mean functions in a regression, or random effects distributions for patients administered treatment combination X. An appropriate probability model for the random distributions should allow dependent but not identical probability models. We focus on the case of the random measures, i.e., the random functions are probability densities and discuss two alternative probability models for such related random measures. One approach uses a decomposition of the random measures into a part which is in common across all levels of X, and offsets which are specific to the respective treatments. The emerging structure is akin to ANOVA where a mean effect is decomposed into an overall mean, main effects for different levels of the categoricatl covariate, etc. We consider computational issues in the special case of DP mixture models. Implementation is greatly simplified by the fact that posterior simulation in the described model is almost identical to posterior simulation in a traditional DP mixture model, with the only modification being a constraint when resampling configuration indicators commonly used in DP mixture posterior simulation. Inference for the entire set of random measures proceeds simultaneously, and requires no more computational effort than the estimation of one DP mixture model. We compare this model with an alternative approach based on modeling dependence at the level of point masses defining the random measures. We use the dependent Dirichlet process framework of MacEachern (2000). Dependence across different levels of the categorical covariate is introduced by defining an ANOVA like dependence of the base measures which generate these point masses. As in the general DDP setup implementation is no more difficult than for a traditional DP mixture model, with the only additional complication being dependence when resampling multivariate point masses. We discuss differences and relative merits of the two approaches and illustrate both with examples.

Pietro Rigo and Patrizia Berti

Uniform approximation of predictive distributions via empirical distributions

 

Given a sequence {Xn} of random variables, with values in a Polish space S and adapted to a filtration {Á n}, let m n(× ) = (1/n)å i=1,...,nI{XiÎ × } be the empirical distribution and

an(× ) = P(Xn+1Î × |Á n)

the predictive distribution. When studying empirical processes for non independent (or non ergodic) data, it is not always appropriate to compare m n with a fixed probability measure, like P(X1Î × ) in case the Xn are identically distributed. Instead, it looks more reasonable to contrast m n with some random probability measure, and two natural candidates are an and bn = (1/n)å i=1,...,nai-1. Indeed, an is the basic object in Bayesian predictive inference. Hence, it is important that good approximations for an are available, and this leads to investigate the asymptotic behaviour of (m n an). In its turn, (m n bn) plays some role in various fields, including stochastic approximation, calibration and gambling.

In this framework, one question is whether

(1) SupEÎ Á |m n(E) an(E)| ® 0 a.s. or SupEÎ Á |m n(E) bn(E)| ® 0 a.s.

where Á is some class of Borel subsets of S (such that the involved random quantities are measurable). In case S = [0,1], one more problem is to find constants cn and dn, possibly random, such that the processes

(2) cn[Fn An] or dn[Fn Bn] converge in distribution

(with respect to Skorohod distance), where Fn, An and Bn are the distribution functions corresponding to m n, an and bn, respectively.

In this talk, problems (1) and (2) are discussed, some results are stated, and a few open problems are mentioned. Among others, one result is that, in order to SupEÎ Á |m n(E) an(E)| ® 0 a.s., it is enough that

(*) SupEÎ Á |m n(E) m (E)| ® 0 a.s. for some random probability measure m ,

(**) P(XjÎ × |Á n) = P(Xn+1Î × |Á n) a.s. for all j > n ³ 1.

Furthermore, when S = Â k, condition (*) alone implies SupEÎ Á |m n(E) bn(E)| ® 0 a.s. for various significant choices of Á . Apart from such result, both (*) and (**) have autonomous interest, and thus are briefly analysed. In particular, for S = Â and Á = {(- ¥ ,t] : t Î Â }, those sequences {Xn} satisfying (*) are characterized. Moreover, when Á n = s (X1,...,Xn), it is proved that {Xn} is exchangeable if and only if it is stationary and (**) holds, some limit theorems under (**) are obtained, and examples of non exchangeable sequences satisfying (**) are exibhited. Finally, with reference to problem (2), suppose S = [0,1], Á n = s (X1,...,Xn) and {Xn} is exchangeable. Then, the probability distributions of Ö n [Fn Bn] weakly converge to a mixture of Brownian bridges.

Gareth Roberts and Omiros Papaspiliopoulos

Bayesian inference for stochastic volatility processes of Ornstein-Uhlenbeck type driven by Levy process noise

The recent RSS read paper by Shephard and Barndorff-Nielsen introduced a flexible family of models which are particularly useful for stochastic volatility processes in finance. Data is assumed to consist of discrete observations from the model

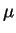
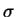
dXt = $\displaystyle \mu$(t)dt + $\displaystyle \sigma$(t)dBt

where $ \sigma^{2}_{}$(t) denotes the stochastic volatility process. According to the Shephard and Barndorff-Nielsen paper, Bayesian inference for these processes remains an open problem. In fact it turns out that the most obvious ways to implement MCMC on these models leads to algorithms which have extremely poor mixing problems, especially for long time series or sparsely observed series.

This talk will introduce two approaches to parameterising the model in terms of marked point processes. The more sophisticated of these manages to break down the correlation structure between the unobserved latent process and its hyperparameters. This leads to MCMC methodology which is fairly robust to the scarcity and length of the observed time series.

Examples to simulated data and financial time series will be given.

Maria Teresa Rodriguez Bernal and Mike Wiper

Bayesian inference for a software reliability model given metrics information

In this article, we are interested in estimating the number of bugs contained within a piece of software code. In the literature, two types of software testing strategy are usually considered. One strategy is to measure various characteristics, or metrics of the code, for example the number of lines or the maximum depth of nesting, and then to try to relate these to measures of code quality such as fault numbers. One model that has been considered, given data for various pieces of code, is regression of the number of faults against the metric data. A second testing strategy is to record times between failures of the code and use this data (given a software reliability model) to make inference about fault numbers. Our objective here is to combine the two sources of information (metrics and failure times) and use a Bayesian model to estimate fault numbers. Inference relies upon Gibbs sampling methods.

Renata Rotondi and Elisa Varini

Bayesian inference for combination of stress-release and epidemic models. Case study: Calabrian Arc

A new class of models has been recently proposed for earthquake occurrences. This class encompasses features of different models, the stress-release and the epidemic-type one, used in hazard analysis to characterize earthquake catalogues. It offers the potential for a unified approach to the analysis and description of different behaviour of the seismic activity. Maximum likelihood estimation for the model parameters are presented in Schoenberg and Bolt (BSSA, 90, 4,2000). We present a bivariate version of these models in the Bayesian framework; MCMC methods are used to estimate the model parameters. Examples to the activity of some Italian seismogenic zones located in the Calabrian Arc are given.

Bruno Sansò

Combining Ground Observations with Output from Dynamic Models for Environmental Variables

We consider the problem of combining observations of environmental variables from ground based stations with output from deterministic dynamic models. Deterministic models usually provide results that correspond to spatial averages over fairly large grid cells, whilst models for ground observations usually consider pointwise realisations of spatial random fields. The combination of these two scales is the main challenge of our application. We consider two applications. In the first one we develop the theory required for the proposal of an environmental standard based on stochastic assumptions on the distribution of a pollutant. We assume that the layout of the network is based on the results of an atmospheric dispersion model and that the standard takes into account the population density. In the second application we combine a purely stochastic approach method to represent rainfall variability in space with purely deterministic regional climate model predictions. We use a truncated normal model to fit the observed point values and the posterior distribution of the model parameters is obtained by using a Markov chain Monte Carlo method.

Scott Schmidler

Bayesian Modeling of Sequences with Non-Local Dependency Structure

We describe a class of probability models for capturing non-local dependencies in sequential data, motivated by applications to biopolymer (protein and nucleic acid) sequence analysis. These models generalize previous work on segment-based stochastic models for sequence analysis. We provide algorithms for Bayesian inference on these models via dynamic programming and Markov chain Monte Carlo simulation. We demonstrate this approach with an application to protein structure prediction.

Refik Soyer and Suleyman Ozekici

Bayesian inference for Markov modulated counting processes with applications to software reliability

In this talk we present a Markov modulated counting process to model software failures in the presence of an operational profile. The model arises in software engineering where a software system is used under a randomly changing operational process. In such systems, the failure characteristics depend on the specific operation performed. We discuss several issues related to software reliability assessment and develop Bayesian inference for the model using Markov chain Monte Carlo methods.

Aad van der Vaart

Asymptotics of infinite-dimensional posteriors

We discuss rates of convergence of posterior distributions in problems with infinite-dimensional parameter spaces. Besides a review of results obtained in the past few years, we hope to present results on model selection and adaptation, and the behaviour of posteriors under misspecification. We may also relate these results to the behaviour of penalized minimum contrast estimators.

Darren J. Wilkinson

Block sampling strategies for the Bayesian analysis of some discretely observed diffusion processes

A diffusion process is governed by the stochastic differential equation (SDE)

dX(t) = a(X(t), t)dt + b(X(t), t)dW(t),

where W(t) is a standard Wiener process. This is a flexible class of models for continuous-time Markov processes with continuous sample paths. Observations on such processes can usually only be made at a finite number of time points, t1, t2,..., tn, and will often be subject to measurement error. This presentation is concerned with the development of efficient strategies for carrying out Bayesian inference for the parameters of these processes in a selection of special cases, based on block-MCMC samplers.

In many cases, techniques for exact conditional simulation of Gaussian systems may be used to simulate realisations of the unobserved process conditional on the model parameters and observed data. Using this as a starting point, block samplers for Bayesian inference may be developed which do not suffer from the problems of very poor mixing exhibited by more naive MCMC approaches.

For several important special cases, the induced discrete-time process, X(t1), X(t2),..., X(tn), is an analytically tractable Gaussian process. For example, the generalised Wiener process, governed by the SDE

dX(t) = a dt + b dW(t)

induces the discrete-time process

(X(tk + 1)| X(tk) = x) $\displaystyle \sim$ N(x + a(tk + 1 - tk), b2(tk + 1 - tk)),

which is a tractable linear Gaussian system. Similarly, the Gaussian Ornstein-Uhlenbeck (OU) process

dY(t) = - $\displaystyle \lambda$Y(t) dt + $\displaystyle \sigma$ dW(t)

induces the AR(1) process

(Y(k + 1)| Y(k) = y) $\displaystyle \sim$ N$\displaystyle \left(\vphantom{e^{-\lambda}y,\frac{\sigma^2(1-e^{-2\lambda})}{2\lambda}}\right.$e- $\scriptstyle \lambda$y,$\displaystyle {\frac{\sigma^2(1-e^{-2\lambda})}{2\lambda}}$ $\displaystyle \left.\vphantom{e^{-\lambda}y,\frac{\sigma^2(1-e^{-2\lambda})}{2\lambda}}\right)$

for integer k. In cases such as these, techniques for filtering, smoothing and simulation-smoothing of dynamic linear state-space models can be used to simulate exact realisations of the unobserved process given noisy observations, and these may be used as the basis for block sampling algorithms for the model parameters. Also, for processes derived from these, such as geometric Brownian motion and the geometric Gaussian OU process, use may be made of the logarithmic transformation for simulation and computation.

Even in cases where the induced discrete-time process is not tractable, it is sometimes possible to transform the process to one that may be approximated in Eulerian fashion by a discrete-time linear Gaussian system. This approximate system will contain many more latent variables than observations, and this ``missing data'' can lead to poor mixing of naive samplers. Fortunately, the use of block samplers can alleviate such problems.

The presentation will give an outline of the construction of block samplers for a selection of diffusion processes (including a bivariate process), and then examine the performance of such samplers in practice.

Don Ylvisaker

Updating Bayesian Numerical Analysis

In an article in the Fourth Purdue Symposium, Diaconis dates Bayesian numerical analysis to (at least) Poincaire in 1896. He goes on to review a variety of contributions to the area, especially to problems of interpolation and quadrature. A part of the early literature came about naturally through statistical concerns but, since the early 1980's, much work has been done in information-based complexity theory under the heading of average case analysis of algorithms (for the explicit connection between the two schools of thought, see Kadane and Wasilkowski's Bayesian Statistics 2 article).

The talk provides a review of some recent results and it points in directions, and to problems, that are of interest to statisticians.

Some ``weird'' formulas are due to bugs in the software transforming Latex and Word into HTML.