Fourth Workshop on

BAYESIAN INFERENCE IN STOCHASTIC PROCESSES

Villa Monastero, Varenna (LC), Italy

June, 2-4, 2005

POSTERS

Posters will be displayed on boards of size 2 meters x 1 meter to be used by two presenters. Therefore each presenter has a 1 x 1 (meter) space.

Carlos Almeida and Michel Mouchart

Bayesian encompassing test under partial observability: General Theory (with application to binary observability)

In the framework of Partial observability, a Bayesian encompassing procedure is proposed in order to compare a parametric model against a (non-parametric) alternative; this paper considers the partial observability process completely known. The general procedure is illustrated by the case where only the sign is observable, and more generally when the available data come from a binary reduction of a vector of latent variables.

Maria Concepcion Ausin and Hedibert Lopes

Large claims approximation in insurance risk processes

Large claims can have a dramatic effect in the analysis of insurance risk processes. For example, the ruin probability for a given initial capital can be underestimated if an inappropriate model is considered for the claim size distribution. Frequently in the literature, large claims are fitted with long-tailed distribution (i.e. with tails that decay more slowly than exponentially) such as the Pareto and the Weibull. However, risk models with long-tailed claim sizes tend to be difficult to analyze and there are not explicit expressions for the ruin probabilities that are often approximated with simulation methods. Alternatively, in this work, we consider flexible models for the claim sizes based on mixtures of distributions. We develop Bayesian inference for a reparametrization of mixtures of Erlang distributions including a non informative prior, which allows us to approximate long-tailed distributions by increasing the number of components in the mixture. Explicit evaluations of the ruin probabilities are possible as the Erlang mixture belong to the set of distributions of phase type. We show how to estimate the ruin probability in different risk reserve processes such as the classical compound Poisson risk process and the Sparre Anderse process. We illustrate this approach with simulated and real data.

Paloma Botella, M. Cambra and Antonio Lopez Quilez

Bayesian Inference on a Cox Model for Epidemiology of Plant Viruses

Cox point process, or doubly stochastic, is a hierarchical model whose events appear by means of a random intensity function. It provides high flexibility in modelling complex phenomena, though inference can be difficult if probabilities in both levels are not parametrically related.
In this work we carry out the spatial analysis of the infected trees by Sharka (Plum Pox Virus) in a parcel of peach trees. Geographic coordinates of the 53 trees that became infected in a 8900 trees parcel can be considered as a point pattern. The infection of these trees could come from a contiguous parcel, in which after detecting the virus the plantation was eliminated. This hypothesis is included through an inhomogeneous point process modelling, based on the distance of the infected trees to the previously infected parcel. Wind direction is incorporated in the analysis implying a random intensity of the infection process.
A Cox model is used to model this problem, with a first level that would gather the possible directions of infection and a second level that would relate the infection to the distance to the contiguous parcel in each direction. The analysis of the model has been made by means of the WinBUGS program.

Javier Cano, David Rios Insua and Carla Tello

BRAMS. A system for Bayesian Reliability, Availability and Maintenance Support

We describe BRAMS a system for Bayesian Reliability, Availability and Maintenance Support that we are developing with the software engineering industry in mind. The system includes modules referring to RBDs, CMTCs and Sofwtare reliability growth models, interlinked. Several examples will be shown.

Roberto Casarin

Inference on diffusion processes by population Monte Carlo method

Diffusion processes are widely used in many fields like physics, engineering, biology, economics and finance. In finance they allow to describe the evolution over time of many financial quantities, like interest rates, asset returns and volatility. The dynamic of a diffusion process can be described by means of a stochastic differential equation (SDE), which could depend on some usually unknown parameters and unobserved components.

In the literature many estimation approaches have been proposed and simulation based methods result particularly useful when dealing with nonlinear SDE. Elerian, Chib and Shephard [5] apply MCMC method to likelihood inference for nonlinear diffusion processes following the high frequency augmentation (HFA) method which has been independently proposed by Jones [13] and Eraker [6]. Billio, Monfort and Robert [1], through an example, apply simulated likelihood ratio method to diffusion processes. Johannes and Polson [11] give an updated review of the MCMC methods for inference on diffusion processes also with partially observed components, with application to finance. Within the simulation based inference framework the Bayesian approach has been widely applied in many recent studies, due the natural way the Monte Carlo approximation can enter in the inference procedure. Moreover the Bayesian framework allows to account also for nonstationarity of the model and for prior information about the parameters. The need for on-line data processing and for more efficient simulation techniques gave rise in the last years to the use of sequential importance sampling methods and of adaptive MCMC methods. See Doucet, de Freitas and Gordon [4] and Robert and Casella [17] for an introduction to general simulation methods and see for example Golightly and Wilkinson [7] and Johannes, Polson and Stroud [12] for recent advances on diffusion process inference.

This work deals with Bayesian simulation based inference for SDE, when observations from the continuous time process are available at regularly spaced discrete time points. In order to make inference on the diffusion process we apply the Euler-Maruyama method and obtain a discretisation of the SDE. Furthermore, in the Bayesian approach parameters are random quantities and once the prior distribution has been chosen, the Bayesian estimator is a function of the posterior distribution. For complex models the estimator is not available in a closed-form, thus a numerical approximation is needed.

The first aim of the work is to propose the iterated importance sampling method (see Guillin, Marin and Robert [8]) as efficient alternative to MCMC method for SDE parameter estimation. In particular we show how the iterative importance sampling method, also called Population Monte Carlo (PMC) method, due to Celeux et al. [3], Capp´ et al. [2], can improve Bayesian parameter estimation and reduce the computational effort.

The second aim is to compare basic and weighted PMC estimators and to study the optimal size of the particle sample at each iteration of the importance sampling algorithm.

Finally we combine the PMC with the HFA method and provide some simulation results for inference on the geometrical Brownian motion and constant elasticity volatility process (see Hull and White [9] for a financial application), with particular attention to the Ornstein-Uhlenbeck and square root mean reverting processes.

[1] M. Billio, A. Monfort and C.P. Robert. The Simulated Likelihood Ratio Method, Doc. du Travail Crest, INSEE, Paris, 1998.
[2] O. Cappe, A. Guillin, J.M. Marin and C.P. Robert. Population Monte Carlo, J. Computational and Graphical Statistics, to appear, 2002.
[3] G. Celeux and J.M. Marin and C.P. Robert. Iterated importance sampling in missing data problems, Cahiers du Ceremade, N. 0326, Univ. Paris Dauphine, 2003.
[4] A. Doucet, N. de Freitas and N.J. Gordon. Sequential Monte Carlo Methods in Practice, Springer-Verlag, New York, 2001.
[5] O. Elerian, S. Chib and N. Shephard. Likelihood inference for discretely observed nonlinear diffusions, Econometrika, 69(4), 959-993, 2001.
[6] B. Eraker. Markov Chain Monte Carlo Analsyis of Diffusion Models with Applications to Finance, Journal of Business and Economics Statistics, 19, 177-191, 2001.
[7] A. Golightly and D.J. Wilkinson. Bayesian Sequential Inference for Nonlinear Multivariate Diffusions, Working paper, University of Newcastle, 2004.
[8] A. Guillin, J.M. Marin and C.P. Robert. Estimation bayesienne approximative par echantillonnage preferentiel, Revue Statist. Appliquee, to appear, 2004.
[9] J. Hull and A. White. The pricing of Options on Assets with Stochastic Volatility, Journal of Finance, Vol. 42, pp. 281-300, 1987.
[10] Y. Iba. Population-based Monte Carlo algorithms, Trans. Japanese Soc. Artificial Intel l., 16(2):279-286, 2002.
[11] M. Johannes and N. Polson. MCMC Methods for Financial Econometrics. To appear in Handbook of Financial Econometrics, Y. Ait-Sahalia and L. Hansen eds, 2004.
[12] M. Johannes, N. Polson and J.R. Stroud. Nonlinear Filtering of Stochastic Differential Equations with Jumps, Working Paper, 2004.
[13] C.S. Jones. Bayesian Estimation of Continuous Time Finance Models, Working Paper, Rochester University, 1998.
[14] I. Karatzas and S.E. Shreve. Brownian Motion and Stochatic Calculus, 2nd Ed., Springer Verlag, New York, 1991.
[15] P.E. Kloeden and E. Platen. Numerical Solution of Stochastic Differential Equations, Springer Verlag, Berlin Heidelberg, 1992.
[16] D. Revuz and M. Yor. Continuous Martingales and Brownian Motion, 3rd Ed., Springer Verlag, Berlin Heidelberg, 1999.
[17] C.P. Robert and G. Casella. Monte Carlo Statistical Methods, 2nd Ed., Springer Verlag, New York, 2004.
[18] M. Tanner and W. Wong. The calculation of posterior distributions by data augmentation. Journal of the American Statistical Association, 82, 528-550, 1987.

Maria Eugenia Castellanos, Javier Morales, Roland Fried and Carmen Armero

A Bayesian walk through the Machine Interference Problem

The machine interference problem is the most popular queueing model with a finite population of customers. Because most applications of this model occur in management and industrial processes, its description is usually presented as a system with working machines (the customers) and operators (the servers). When a machine breaks down and there is at least one operator idle the machine is repaired immediately. The machine needs to wait for service otherwise. Basically, repair times and machine life times are assumed to be independent and exponentially distributed. The Bayesian analysis of the model is oriented towards evaluation of staffing levels and system efficiency. This includes prediction of general congestion measures of the system in equilibrium, such as the number of machines which are down or the time necessary to put an out of order machine into operation again, and more specific measures like the net production rate and the machine availability.

Aart F. de Vos and Marc K. Francke

Marginal Likelihood, Jeffreys' Rule and Unit Root Tests

In inference on the covariance matrix of the general linear model, the regression and scale parameters are nuisance. Classical marginal likelihood is known as a good way to get rid of these parameters. We argue that the same likelihood can also be used in Bayesian inference, directly or by application of the independence Jeffreys' prior. The latter differs from Jeffreys' rule, while reference priors are ambiguous. In case only one parameter describes the covariance structure, classical tests based on marginal likelihood ratio are uniformly most powerful invariant (UMPI) if this ratio is a monotone function of some statistic. For this case we show that model choice based upon Bayes Factors corresponds to a classical test with a size determined by prior considerations. The data are used in the same way.
Our example is the much discussed unit root model where we obtained tests that are almost UMPI using classical marginal likelihood, while Bayesian inference based upon Jeffreys' rule fails. Essentially the same test may be obtained from a Bayesian analysis using independence priors. The correspondence between its size and the prior however is complex, specifically in relation to the sample size; it is studied for the AR(1)-model.

Vanja Dukic, B. Elderd and G. Dwyer

A Bayesian SEIR approach to modeling smallpox epidemics

Much of the recent US public-policy debate regarding smallpox vaccination has focused on mass versus trace vaccination strategies; namely, whether the public can be better protected by vaccination of the entire population or of only those who have been in contact with infected individuals. Much of the previous work on smallpox epidemics has generally employed relatively complex deterministic models, with many biological parameters fixed, and focusing mostly on a single point estimate of the disease reproductive rate (the number of newly infected individuals arising from a single infected individual). We present a Bayesian analysis of the multiple historical smallpox epidemics that yields an estimate of the distribution of the disease reproductive rate, taking into account the uncertainty of all other parameters in the model, as well as population and geographical heterogeneity. We then present a comparison of the two vaccination strategies based on the posterior predictive distribution of the outcomes under several scenarios.

Marc K. Francke and Aart F. de Vos

Marginal Likelihood in State Space Models

In this paper we examine different formulations of the likelihood in the general linear model from Bayesian and classical viewpoints. Starting point is the diffuse Kalman filter. This is an essentially Bayesian "trick" to compute estimates of parameters and the likelihood function running a filter. It is specifically useful to cope with diffuse initial conditions, or as Bayesians call it, improper priors. There is a problem however in the resulting formula, caused by the fact that a likelihood is degenerate in such a case. This makes one question the validity of the derivation. Indeed there appears to be a snag, but for many purposes not a serious one. But there are examples where the diffuse likelihood differs among reformulations of the same model. The solution is to use the marginal likelihood. The classical concept goes back to Harville, 1974, the Bayesian equivalent results by using Jeffreys Independence priors. We give the simple adjustments needed in the diffuse Kalman filter to get the marginal likelihood and discuss applications and problems with nonlinear models.

Pilar Gargallo and M. Salvador

Monitoring for Models of the Exponential Family. A Bayesian Decision Approach

This paper proposes an algorithm for monitoring two-sided changes in mean of series from the exponential family. The adopted approach is bayesian and uses a loss function which take into account the run lengh extending the monitoring scheme proposed in Harrison and Veerapen (1994). The algorithm is illustrated with several examples in which the power of the monitor is analized.

Alessandra Guglielmi, Ilenia Epifani and Eugenio Melilli

Distributional results for functionals of Dirichlet processes

A fundamental problem in a nonparametric Bayesian framework is the computation of the laws of functionals of random probability measures. For instance, in this context, inference about the variance of the frequency distribution of a characteristic in a population requires the knowledge of its posterior distribution. The aim of this work is to show some new results concerning the law of the functional variance V of a Dirichlet process P, which can be considered quite general to some extent. For instance, we will see that the law of the variance of Dirichlet mixtures of location-invariant densities is a mixture of distributions of random Dirichlet variances. We establish a simple distributional relationship between V and the random variable (X-Y)^2, where X and Y are independent copies of the random mean of the Dirichlet process P. Useful expressions for some integral transforms of V are also obtained and illustrative examples are given. Finally, some classes of moment-based distribution approximations will be reviewed and an application to the posterior law of V will be illustrated.

Konstantinos Kalogeropoulos, Gareth O. Roberts and Petros Dellaportas

Bayesian Inference for Stochastic Volatility Diffusion Models Using Time Change Transformations

This paper presents a new Markov chain Monte Carlo approach for diffusion driven stochastic volatility models. The algorithm is based on a data augmentation scheme where we treat both the paths of the unobserved volatility and the paths between any two observed points as missing data. We use a time change transformation to break down the dependence between the diffusion parameters and the transformed paths. We then present an appropriate Markov chain Monte Carlo algorithm to sample from the posterior of the diffusion paths and the parameters of the stochastic volatility model.

Theodore Kypraios and Gareth O. Roberts

A semi-Parametric Time Series Model Based on Latent Branching Trees

A branching process is used to introduce a class of semi-parametric time series models. We describe in detail how one can construct such a branching process and we list the model's properties. Markov Chain Monte Carlo methods are adopted to make inference for the parameters. Furthermore, Non-Centered and partially Non-Centered parameterisations are also presented in order to improve the mixing of the Markov chain. This is work is based on Neal (2002, Bayesian Statistics, 7).

John C. Liechty, Merrill W. Liechty, Campbell Harvey and Peter Muller

Asset allocation using dynamic linear models with skewed elliptical errors

The mean variance framework proposed by Markowitz for determining optimal asset allocation (how to form an optimal investment portfolio) makes several unrealistic assumptions. Recent work in the area of asset allocations has relaxed several of these assumptions, including explicitly accommodating parameter uncertainty in the estimation procedure and considering i.i.d. probability models with higher order moments (i.e. the Skewed Gaussian density). In this paper, we explore relaxing the i.i.d. assumption by solving the asset allocation problem under the assumption of a number of competing dynamic models. The class of models is based on a dynamic linear model with Skewed Elliptical errors. We discuss the performance of this dynamic asset allocation approach with the competing methods which are widely used in the practice and discuss the idea of risk profiles as an alternative approach for determining an asset allocation scheme for a class of reasonable of utility functions.

Ales Linka and Petr Volf

Segmentation of texture with local MRF models

The contribution deals with the analysis of textures and their MRF models. It is assumed that in different parts of texture the parameters of model may differ. The objective is to find these areas (and model parameters), i.e. to segment the texture with respect to local models. In the Bayes scheme, for given number of different models (K), we combine the priors of parameters, the Potts MRF of local values of parameters (it supports the connectivity of areas with the same models) and pseudo-likelihood of data, given the configuration of models. Solution is then obtained from the MH algorithm, parameter of Potts model is used as a tuning parameter. However, as we search for an optimal configuration of models (not for representation of posterior), the search may be simplified and solved with the aid of simulated annealing. The same concerns the case with unknown K: Instead of full RJ MH procedure, it suffices to compare optimal results for different K, penalized by corresponding priors. The application deals with the detection of nonhomogeneous spots (e.g. of poor quality) in digitized image of non-woven textile material.

Antonio Lopez-Quilez, Carmen Armero and Rut Lopez-Sanchez

Bayesian Analysis of the Time to Diagnosis after an Abnormal Screening Mammography

Breast cancer is one of the diseases with more impact on health in women. Its prediction basically depends on the extension of the damage at the detection time. Consequently, an early diagnosis is the better way to improve the possibilities of a recovery. In the Pais Valencia, one of the Spanish autonomous regions that has taken on the management of all health services, the Breast Screening Programme has been designed to detect unsuspected cancer in healthy women. This study focus attention on women with an abnormal screening mammography taking part in this programme during year 2002. Specifically, we are interested in comparing the length of the times to diagnosis in connection with the different medical procedures performed, main women risk factors and hospitals taking part in the program. Generalized linear mixed models are used in order to incorporate random effects characterizing heterogeneity among hospitals. Bayesian reasoning and Markov Chain Monte Carlo simulation are considered for estimation and inference.

Lászlo Márkus and Miklos Arato

A Inhomogeneous Spatial Poisson Process for Modelling Car Insurance Data

The results of the analysis of spatial dependence structure for claims occuring in third party liability car insurance in Hungary is going to be reported. An inhomogeneous spatial Poisson process is fitted to the data. Presently the following model fit is obtained for 168 subregions of the country by an MCMC approach. The conditional intensity of the Poisson process is $ \lambda$ . e($\scriptstyle \theta_{i}$ . ti) with $ \lambda$ being the common claim frequency, ti the overall time-at-risk of all policyholders at the i-th region, and $ \theta_{i}^{}$ the local risk factor. The vector of all local risk factors $ \Theta$ = ($ \theta_{i}^{}$, i = 1,..., 168) is supposed to be distributed normally, with 0 mean and a variance matrix $ \Sigma$ of two parameters $ \tau^{2}_{}$,$ \rho$:

$\displaystyle \Sigma$ = $\displaystyle {\frac{{1}}{{\tau^2}}}$(I - $\displaystyle \rho$ . A)-1

where A is the neighbourhood matrix of zeros and ones, with 1 at the (i,j) position indicating the i-th and j-th subregions to be neighbours. Supposing $ \tau^{2}_{}$ and $ {\frac{{\rho}}{{\rho_{max}}}}$ to be distributed respectively as $ \Gamma$($ \alpha$,$ \beta$), and Beta(p, q) sufficiently adequate fit can be achieved even by a simple Metropolis-Hastings algorithm. However, when risks for all the 3112 settlements of Hungary are considered separately the algorithm needs unacceptedly long time to stationarise. Also, the fit is intended to be carried out simultaneously for other risk parameters such as sex, age and car type. The dependence of the solution on priors is also a problem to be addressed.

Miguel Ángel Martínez Beneito, Oscar Zurriaga Llorens, Hermelinda Vanaclocha Luna, Antonio López Quílez, Carmen Armero, David Conesa, Juan José Abellán Andrés and Jordi Pérez Panadés

Parametric and Semi-Parametric Approaches to Bayesian Survival Analysis with Spatial Term

Bayesian inference allows to incorporate a great variety of information and structures when modelling survival times of a given specific population. In particular, recent applications in this topic introduce spatial information about patients at different levels of aggregation. In general, parametric and semi-parametric approaches are the two main ways to include spatial information in a survival study. In this work, both techniques are used to evaluate sojourn times of patients with renal diseases from the Comunidad Valenciana Renal Registry. Covariates as age, sex, treatment or period are included, and geographical residence is also incorporated in the analysis. Discussion about advantages and limitations of each one of these approaches are presented. In particular, semi-parametric procedure has the advantage of considering dynamic covariates properly.

William J. McCausland

Time Reversibility of Stationary Regular Finite State Markov Chains

We propose an alternate parameterization of stationary regular finite-state Markov chains, and a decomposition of the parameter into time reversible and time irreversible parts. We demonstrate some useful properties of the decomposition, and propose an index for a certain type of time irreversibility. Two empirical examples illustrate the use of the proposed parameter, decomposition and index. One involves observed states; the other, latent states.

Loukia Meligkotsidou and Paul Fearnhead

Ancestral inference in population genetics via importance sampling

Population genetics is concerned with analysing a sample of DNA sequences taken from individuals of a population. A genealogical tree can be constructed to represent the ancestry of the sample. Coalescence or branching events in the tree correspond to individuals in the genealogy sharing a common ancestor. The mutation model assumes that mutations occur as events in a Poisson process, with each new mutation occurring at a site that hasn't experienced mutation before.
Ancestral inference in population genetics involves estimating the branching times in genealogical trees. Under the natural coalescent prior on the branch lengths the posterior distribution of the coalescence times is difficult to handle. We propose using a non-informative phylogenetic prior on the branch lengths and following the approach of Fearnhead and Meligkotsidou (2004) to approximate the posterior distribution of coalescence times. Then we correct for the true posterior distribution via Importance Sampling. We show how this approach can be applied to deal with a class of coalescent models.

Alicia Quiros Carretero, Raquel Montes and Juan Antonio Fernandez

Bayesian Inference in functional Magnetic Resonance Imaging

Functional magnetic resonance imaging (FMRI) is a technique that creates images of a subject\222s brain that are sensitive to changes in blood oxygenation, caused by neural activation. We are interested in identifying those brain activity regions by observing the differences in blood magnetisation due to the haemodinamic response. The data sets produced by an fMRI experiment are typically very large and therefore computationally expensive. A typical output from an fMRI experiment might consist of voxel data points, modelled by a general linear model. t-test are usually performed to look for significantly activated areas, adjusted to allow for multiple comparisons. Using a Bayesian framework provide us with the ability to probabilistically incorporate prior information by modelling the pattern as a Markov Random Field (MRF). To correctly infer on parameters of interest, for example, the haemodynamic response function parameters is not an easy task giving the complexity of the model. Monte Carlo Markov Chain (MCMC) methods enable sampling from the posterior distributions of interest to give estimates of the summary statistics.

Diego Salmeron and Juan Antonio Cano

Regularized particle filter for Bayesian estimation in unobserved diffusion processes

In this work we study the goodness of an approximation based on Euler schemes for Bayesian estimation of the parameters appearing in a stochastic differential equation. We consider statistical models in which the observations are related with an unobserved diffusion in a nonlinear way. Although the Euler approximation jointly with a Gibbs sampler and a Metropolis-Hastings algorithm ia a good methodology for Bayesian inference in this model, it is known that the rate of convergence of the Gibbs sampler can be arbitrarily slow if the amount of the augmentation obtained by the Euler discretization, is large. In this paper a simple method for sequential estimation is proposed, based on simulation and regularization, without the use of the Gibbs sampler.

Simo Särkkä, Aki Vehtari and Jouko Lampinen

Rao-Blackwellized Particle Filter for Tracking Unknown Number of Targets in Clutter

We present a new Rao-Blackwellized particle filtering based algorithm for tracking an unknown number of targets in clutter. The algorithm is based on formulating probabilistic stochastic process models for target states, data associations, and birth and death processes. The tracking of these stochastic processes is implemented using sequential Monte Carlo sampling or particle filtering, and the efficiency of the Monte Carlo sampling is improved by using Rao-Blackwellization

Chris Sherlock and Paul Fearnhead

A Gibbs Sampler for the Markov Modulated Poisson Process

We consider the general Markov Modulated Poisson Process (MMPP) where only the Poisson Process is observed, and describe a Gibbs sampler that first samples from the exact conditional distribution of the (hidden) Markov chain. Bayes Factors can be calculated from the Gibbs sampler output, which enables model choice to be performed. The technique is applied to occurences of the Chi site in the E.coli genome. We also examine the mixing properties of various MCMC algorithms over a selection of 2-dimensional MMPP's.

Fabio Spizzichino and Rachele Foschi

An Invariance Property of Spatial Mixed Poisson Processes

It is a very well known result in queueing theory that the output of an infinite server queue Mt/G/$ \infty$ (with a Poisson arrival process, then) is Poisson as well.

Such a closure-type result can be extended in a number of different directions.

Most natural types of extensions can be obtained as follows:

i) by replacing Poisson arrival processes with Mixed Poisson arrival processes

ii) by replacing Poisson arrival processes with M-Poisson processes on the line

iii) by replacing the Mt/G/$ \infty$ model with a more general transformation, where each jump Si in the departure process is obtained by combining an arrival Ti with a random variable Zi:

Zi = $\displaystyle \psi$$\displaystyle \left(\vphantom{ T_{i},Z_{i}}\right.$Ti, Zi$\displaystyle \left.\vphantom{ T_{i},Z_{i}}\right)$

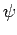
(being $ \psi$$ \left(\vphantom{ T_{i},Z_{i}}\right.$Ti, Zi$ \left.\vphantom{ T_{i},Z_{i}}\right)$ = Ti + Zi, for the specific scheme of an infinite server queue).

Z1, Z2,... are assumed to be i.i.d.

The extension in ii) is preliminary, and turns out to be basilar, for the extension in iii) (see [1]). The latter case can, in its turn, be extended to more general models with spatial Poisson arrival processes.

Substantially such closure-type results are based on the ``Order Statistics Property'' (OSP) of the arrival process (see [2] and [3], for the case in i) and [1] for ii) and iii)).

Also the ``p-thinning Property" of the arrival process (see e.g. [4]) has a fundamental role in this context (see also [5] for some remarks in this concern).

In the talk, we consider models characterized by generic transformations 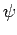$ \psi$ of "spatial-mixed Poisson" arrival processes and present a more general (closure-type) result, that can be obtained in terms of the Order Statistics and p-thinning properties.

Possibly, we also aim to discuss some aspects in the Bayesian estimation of the unobservable parameter M of the spatial-mixed Poisson process {N} ({N} being a conditionally spatial Poisson process, given M).


References

[1] Brown M. (1969). J. Appl. Probability, 6, 453-458.

[2] Huang, W. and Puri, P. (1990). Sankhya, Ser. A, 52, 232-243.

[3] Berg M. and Spizzichino F. (2000). Math. Methods of Oper. Res., 51, 301-314.

[4] Grandell J. (1997). Chapman & Hall, London.

[5] Foschi R. (2005). Tesi di Laurea in Matematica. Universita' "La Sapienza".

Osnat Stramer and Jun Yan

Parametric inference for partially observed diffusion processes: a comparison study

Diffusion models described by stochastic differential equations are used extensively in many areas of science-engineering, hydrology, financial economics and physics. While the models are formulated in continuous-time, the data are recorded at discrete points in time. For most diffusion models the likelihood function is unavailable. We describe four alternative approaches to inference of diffusion models.
  • Bayesian inference using Gibbs sampling and data augmentation (Elerian at al., 2001; Roberts & Stramer, 2001).
  • Simulated maximum likelihood estimation (Pedersen, 1995; Durham & Gallant, 2002).
  • Analytical approximation of the likelihood (Ait Sahalia, 2002 and Ait Sahalia, 2005).
  • Efficient method of moments (Gallant & Long, 1997)
    • All the above methods are computationally heavy. We review all four methods in terms of
  • what models can each method handle,
  • theoretical justification of the method,
  • accuracy,
  • speed.
    • We perform a set of Monte Carlo experiments to compare the performance of these approaches on two different type of models:
  • Simple models like the square-root/Cox-Ingersoll-Ross models that can be solved explicitly and hence can be estimated via maximum likelihood.
  • Models like the preferred model for short term interest rates of Ait-Sahalia (1996) that cannot be solved explicitly and hence cannot be estimated via maximum likelihood.
    • In addition, we also provide a numerical technique to improve the computational efficiency of the simulated maximum likelihood method proposed by Durham & Gallant (2002).

    Paola Tardelli

    Dynamical estimate for lifetimes of particles belonging to a hetereogeneous population

    A heterogeneous population of identical particles, divided into a finite number of classes, according to their level of health, is considered. The partition can change during the time and is not observed. We just observe the cardinality of a particular class. Our aim is to find the conditional distribution of particles lifetimes, given such observation. To this end, we use a Bayesian dynamical approach that is stochastic filtering techniques.

    Stefano F. Tonellato

    Random field priors for spectral density functions

    In this paper we discuss how a Gaussian random field with Matern covariance function can represent prior uncertainty about the log-spectral density, $g(\omega)$, of a stationary time series. Hyperparameters can be suitably tuned in order to determine the mean square differentiability and the range of autocorrelation of the random field $g(\omega)$. However, Bayesian computations cannot be easily performed under such prior elicitation. We suggest therefore to approximate the Gaussian random field priors with a class of Gaussian Markov random fields which preserve most of the smoothness properties of the genuine prior distributions. Such approximation allows us to implement MCMC methods efficiently. Applications to simulated and real data will be shown.

    Matilde Trevisani and Nicola Torelli

    Spatial misalignment modeling for small area estimation problems

    In this paper we specify, within a hierarchical Bayesian setting, appropriate atom-based models to solve the following small area estimation (SAE) questions: (i) combining auxiliary covariates which are available on non nested areal partitions (misaligned areal regression problem); (ii) providing small area estimates by using planned domains data (misaligned areal interpolation problem). To illustrate our approach we consider the problem of estimating the number of unemployed at Local Labour Market area (small area or target zone) level by using two misaligned source data: auxiliary information available on different administrative partitions; reliable estimates of unemployed on Labour Force Survey planned domains. Thus we explore the close connection that typical SAE issues show to have with spatial misalignment problems. Ob ject of SAE is, in fact, inference on survey non-planned "minor domains" (the so called small areas): based on direct domain data (when available), it leads to estimates of poor quality. Thereby models are set up for borrowing strength from indirectly related data sources. Similarly, spatial misalignment models are set up whenever "target zones" for which data are needed are different from source zones on which data are available.

    Mark Van Lokeren and F. Thomas Bruss

    Optimal Stopping for Sequences of Random Variables with Unknown Success Parameter

    Let X_1, X_2, ..., X_n be a finite sequence of identically distributed random variables taking values in {0, 1}. If X_k = 1 for some 1 \leq k \leq n, we say a success is observed at time k. We assume the distribution of X_1 to be a Bernoulli law with unknown success parameter p. Observing the random variables X_1, X_2, ..., X_n sequentially, we want to find a strategy which maximizes the probability of stopping at the last success (if any) in the sequence. No recall on preceeding successes is allowed. We study the case where the prior distribution of p is taken as a Beta law. Using a Bayesian approach to update the prior distribution each time a random variable is observed, we determine an explicit form of the optimal strategy. The strategy relies on a recurrence relation, which also gives the optimal value of the maximum probability of stopping at the last success. The result is a generalisation of [1]. Finally we discuss some applications to clinical trials and sequential search problems.

    [1] F.T. Bruss, Sum the odds to one and stop, Ann. Prob., 28(3) 1384-1391, 2000.

    Petr Volf

    Cluster analysis of time series of Poisson counts

    The paper deals with the statistical analysis of aggregated unemployment data modeled as a time series of Poisson counts. Cluster analysis is employed for selection of sub-populations with similar development of unemployment in Czech Republic in recent years of economic transformation. It is shown how the clusters are connected with certain characteristics (covariates) of these sub-populations. We start from the model-based clustering yielding simultaneously the set of models for distinct clusters and detecting outlied sequences. This methodology still suffers one problem, namely the assessing the number of clusters, though a set of more-less ad-hoc criteria have been proposed. Therefore, we use an alternative based on the consistent Bayes approach, assuming sequential priors for models and taking the number of clusters as a random variable, too. The problem is then solved with the aid of an RJ-MCMC procedure. Further, inside the clusters, an additional analysis of heterogeneity is performed.

    Simon P. Wilson and M. J. Costello

    Predicting Future Discoveries of European Marine Species using a Non-homogeneous Renewal Process

    Predicting future rates of species discovery and the number of species remaining are important in efforts to preserve biodiversity, discussions on rate of species extinction and comparisons on the state of knowledge of animals and plants of different taxa. In this paper, data on discovery dates of species in 32 European marine taxa are analysed using a class of thinned temporal renewal process models. These models allow for both under and over-dispersion with respect to the non-homogeneous Poisson process. An approach for implementing Bayesian inference for these models is described that uses Markov chain Monte Carlo simulation and that is applicable to other types of thinned process. Predictions are made on the number of species remaining to be discovered in each taxon.

    Michael P. Wiper, Maria Concepcion Ausin and Rosa Lillo

    Bayesian control of the number of servers in a GI/M/c queueing system

    In this paper we consider the problem of designing a GI/M/c queueing system. Given arrival and service data, our objective is to choose the optimal number of servers so as to minimize an expected cost function which depends on quantities, such as the number of customers in the queue. A semiparametric approach based on Erlang mixture distributions is used to model the general interarrival time distribution. Given the sample data, Bayesian Markov chain Monte Carlo methods are used to estimate the system parameters and the predictive distributions of the usual performance measures. We can then use these estimates to minimize the steady-state expected total cost rate as a function of the control parameter c. We provide a numerical example based on real data obtained from a bank in Madrid.
    Some ``weird'' formulas are due to bugs in the software transforming Latex and Word into HTML.